Determinants - Revision Notes

 CBSE Class 12 Mathematics

Chapter-4
Determinant

  • A determinant of a square matrix A is denoted by det.A or |A|.
  • A determinant of order 1 x 1 matrix 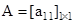is given by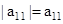 
  • A determinant of order of 2 x 2 matrix A 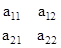is given by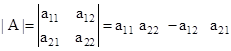 
  • A determinant of order 3 x 3 matrix A 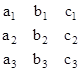is given by (expanding along ( ) 
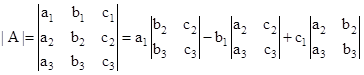
  • We can find the value ofa a determinant by expanding along any one of the three rows (or columns) and the value remains same.
  • Generally, we find the value of a determinant by expanding along a row or column which has maximum number of zeroes.
  • For any square matrix A, the |A| satisfy following properties.
  1. |A′| = |A|, where A′ = transpose of A.
  2. If we interchange any two rows (or columns), then sign of determinant changes.
  3. If any two rows or any two columns are identical or proportional, then value of determinant is zero.
  4. If we multiply each element of a row or a column of a determinant by constant k, then value of determinant is multiplied by k.
  5. Multiplying a determinant by k means multiply elements of only one row (or one column) by k.
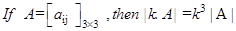
  7. If elements of a row or a column in a determinant can be expressed as sum of two or more elements, then the given determinant can be expressed as sum of two or more determinants.
  8. If to each element of a row or a column of a determinant the equimultiples of corresponding elements of other rows or columns are added, then value of determinant remains same.
  • If A is skew symmetric matrix of odd order, then |A| = 0.
  • Area of a triangle with vertices 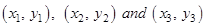 is given by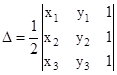 
  • Minors: Minor of an element aij of the determinant of matrix A is the determinant obtained by deleting 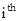 row and 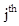column and denoted by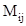 
  • Confactors: Cofactor of aij of given by Aij = (– 1)i+ j Mij.
  • Value of determinant of a matrix A is obtained by sum of product of elements of a row (or a column) with corresponding cofactors. For example, .
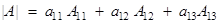  • If elements of one row (or column) are multiplied with cofactors of elements of any other row (or column), then their sum is zero. For example, 
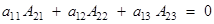
  • Adjoint of a matrix: 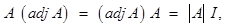where A is square matrix of order n.
  • Singular Matrix: A square matrix A is said to be singular or non-singular according as
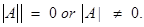
  • Inverse of a square matrix: If AB = BA = I, where B is square matrix, then B is called inverse of A. Also 
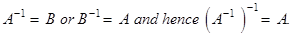
  • A square matrix A has inverse if and only if A is non-singular.
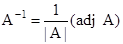
  • If 

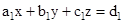
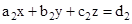
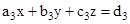
then these equations can be written as AX = B, where

• 

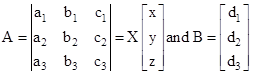
  • Unique solution of equation AX = B is given by 
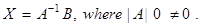
  • A system of equation is consistent or inconsistent according as its solution exists or not.
  • For a square matrix A in matrix equation AX = B

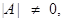• | there exists unique solution

• |A| = 0 and (adj A) B ≠ 0, then there exists no solution

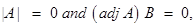•  then system may or may not be consistent and has infinite solutions.