Determinants - Exemplar Solutions
CBSE Class–12 Mathematics
NCERT Exemplar
Chapter - 4
DETERMINATS - Short Answer Questions
1. If 
then find x.
Sol. We have . This gives
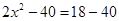
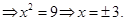
2. If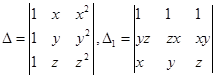 
, then prove that 
= 0.
Sol. We have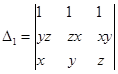 
Interchanging rows and columns, we get
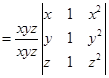
Interchanging C1and C2
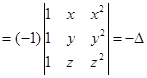
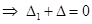
3. Without expanding, show that
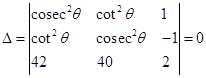
Sol. Applying 
, we have
4. Show that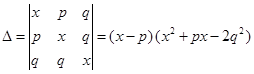 
Sol. Applying 
, we have
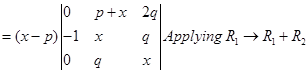
Expanding along 
. We have
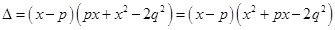
5. If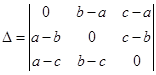 
, then show that 
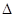is equal to zero.
Sol. Interchanging rows and columns, we get
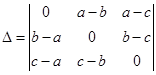
Taking ‘–1’ common from R1, R2 and R3, we get
6. Prove that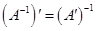 
, where A is an invertible matrix.
Sol. Since A is an invertible matrix, so it is non-singular.
We know that |A| = |A′|. But |A| ≠ 0. So |A′| ≠0 i.e. A′ is invertible matrix.
Now, we know that AA–1= A–1A = I.
Taking transpose on both sides, we get (A–1)′ A′= A′(A–1)′= (I)′ = I
Hence (A–1)′ is inverse of A′, i.e., (A′)–1= (A–1)′
7. If x= – 4 is a root of 
then find the other two roots.
Sol. Applying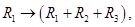 
we get
Taking (x+4) common from R1, we get
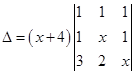
Applying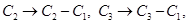 
we get
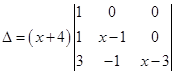
Expanding along R1,
Δ = (x+ 4) [(x – 1) (x– 3) – 0]. Thus, Δ = 0 implies
8. In a triangle ABC, if
then prove that ΔABC is an isoceles triangle.
Sol. Let 
.
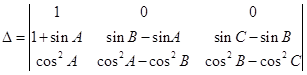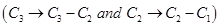
Expanding along R1, we get
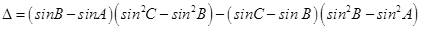
= (sinB – sinA) (sinC – sinB) (sinC – sin A) = 0
⇒ either sinB – sinA = 0 or sinC – sinB or sinC – sinA = 0
⇒ A = B or B = C or C = A
i.e. triangle ABC is isosceles.
9. Show that if the determinant 
then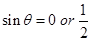 
Sol. Applying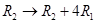 
and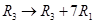 
, we get
or 2 [5 (2 + 7 sin3θ) – 10 (cos2θ+ 4sin3θ)] = 0
or 2 + 7 sin3θ– 2 cos2θ– 8 sin3θ= 0
or 2 – 2cos 2θ– sin 3θ= 0
sinθ(4sin2θ+4sinθ– 3) = 0
or sinθ= 0 or (2sinθ– 1) = 0 or (2sinθ + 3) = 0
or sinθ= 0 or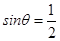 
.
Objective Questions
Choose the correct answer from the given four options in each of the Example 10 and 11.
10. Let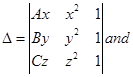 
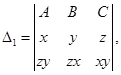then
(A) Δ1= – Δ
(B) Δ ≠ Δ1
(C) Δ– Δ1= 0
(D) None of these
Sol. (C) is the correct answer since 
=
11. If x, y
R, then the determinant 
lies in the interval.
(A) 
(B) [–1, 1]
(C)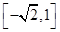 
(D)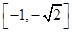 
Sol. The correct choice is A. Indeed applying R3→R3– cosyR1+ sinyR2, we get
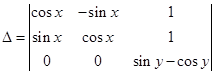
Expanding along R3, we have
Δ = (siny– cosy) (cos2x+ sin2x)
= (siny– cosy) = 
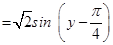
Hence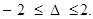 
Fill in the blanks in each of the Examples 12 to 14.
12. If A, B, C are the angles of a triangle, then
Sol. Answer is 0. Apply 
13. The determinant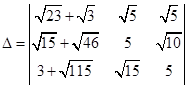 
is equal to ...............
Sol. Answer is 0. Taking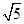 
common from C2and C3and applying 
we get the desired result.
14. The value of the determinant
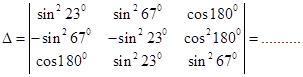
Sol. Δ= 0. Apply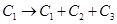 
.
State whether the statements in the s 15 to 18 is True or False.
15. The determinant
is independent of x only.
Sol. True. Apply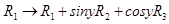 
, and expand.
16. The value of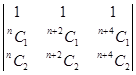 
is 8.
Sol. True
17. If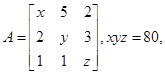 
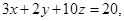then
.
Sol. False.
18. If 
then x= 1, y= – 1.
Sol. True