Linear Programming - Exemplar Solutions
CBSE Class–12 Mathematics
NCERT Exemplar
Chapter - 12
Linear Programming - Objective Type Questions
Choose the correct answer from the given four options in each of the Exercises 26 to 34.
26. The corner points of the feasible region determined by the system of linear constraints are 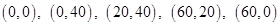 . The objective function is
. The objective function is 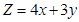 .
.
Compare the quantity in Column A and Column B
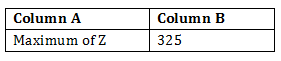
(A) The quantity in column A is greater
(B) The quantity in column B is greater
(C) The two quantities are equal
(D) The relationship cannot be determined on the basis of the information
Supplied
Sol. (B)
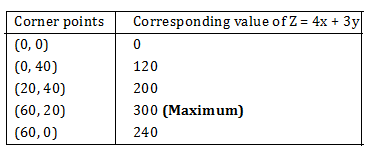
Hence, maximum value of 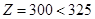 .
.
So, the quantity in column B is greater.
27. The feasible solution for a LPP is shown in Fig. 12.12. Let 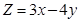 be the
be the
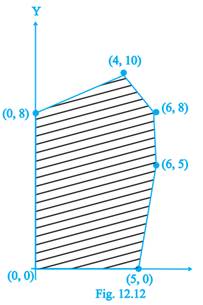
objective function. Minimum of Z occurs at
(A) (0, 0)
(B) (0, 8)
(C) (5, 0)
(D) (4, 10)
Sol. (B)
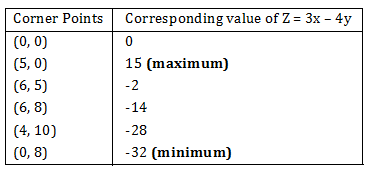
Hence, the minimum of Z occurs at (0, 8) and its minimum value is -32.
28. Refer to Exercise 27. Maximum of Z occurs at
(A) (5, 0)
(B) (6, 5)
(C) (6, 8)
(D) (4, 10)
Sol. (A) Refer to solution 27, maximum of Z occurs at (5, 0).
29. Refer to Exercise 27. (Maximum value of Z + Minimum value of Z) is equal to
(A) 13
(B) 1
(C) –13
(D) –17
Sol. (D) Refer to solution 27, maximum value of Z + minimum value of Z.
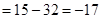
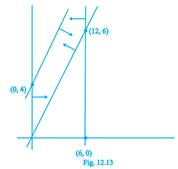
30. The feasible region for an LPP is shown in the Fig. 12.13. Let F = 3x– 4y be the objective function. Maximum value of F is.
(A) 0
(B) 8
(C) 12
(D) –18
Sol. (C) The feasible region as shown in the figure, has objective function F = 3x – 4y

Hence, the maximum value of F is 12.
31. Refer to Exercise 30. Minimum value of F is
(A) 0
(B) –16
(C) 12
(D) does not exist
Sol. (B) Referring to solution 30, minimum value of F is –16 at (0, 4).
32. Corner points of the feasible region for an LPP are 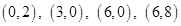 and
and 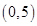 .
.
Let 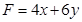 be the objective function.
be the objective function.
The minimum value of F occurs at
(A) (0, 2) only
(B) (3, 0) only
(C) the midpoint of the line segment joining the points (0, 2) and (3, 0) only
(D) any point on the line segment joining the points (0, 2) and (3, 0).
Sol. (D)
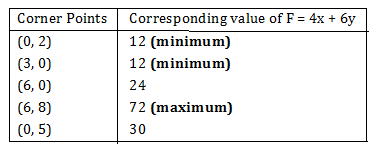
Hence, minimum value of F occurs at any points on the line segment joining the points (0, 2) and (3, 0).
33. Refer to Exercise 32, Maximum of F – Minimum of F is equal to
(A) 60
(B) 48
(C) 42
(D) 18
Sol. (A) Referring to the solution 32, maximum of F - minimum of 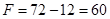 .
.
34. Corner points of the feasible region determined by the system of linear constraints are 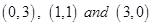 . Let
. Let 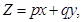 where
where 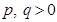 . Condition on p and q so that the minimum of Z occurs at
. Condition on p and q so that the minimum of Z occurs at 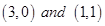 is
is
(A) p = 2q
(B) 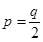
(C) p = 3q
(D) p = q
Sol. (B)

So, condition of p and q, so that the minimum of Z occurs at 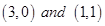 is
is
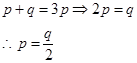
Fill in the blanks in each of the Exercises 35 to 41.
35. In a LPP, the linear inequalities or restrictions on the variables are called _________.
Sol. In a LPP, the linear inequalities or restrictions on the variables are called linear constraints.
36. In a LPP, the objective function is always _________
Sol. In a LPP, objective function is always linear.
37. If the feasible region for a LPP is _________, then the optimal value of the objective function  may or may not exist.
may or may not exist.
Sol. If the feasible region for a LPP is unbounded, then the optimal value of objective function  may or may not exist.
may or may not exist.
38. In a LPP if the objective function 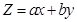 has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same _________ value.
has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same _________ value.
Sol. In a LPP, if the objective function 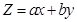 has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same maximum value.
has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same maximum value.
39. A feasible region of a system of linear inequalities is said to be _________ if it can be enclosed within a circle.
Sol. A feasible region of a system of linear inequality is said to be bounded, if it can be enclosed within a circle.
40. A corner point of a feasible region is a point in the region which is the _________ of two boundary lines.
Sol. A corner point of feasible region is a point in the region which is the intersection of two boundary lines.
41. The feasible region for an LPP is always a _________ polygon.
Sol. The feasible region for an LPP is always a convex polygon.
State whether the statements in Exercises 42 to 45 are True or False.
42. If the feasible region for a LPP is unbounded, maximum or minimum of the objective function 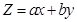 may or may not exist.
may or may not exist.
Sol. True
43. Maximum value of the objective function 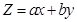 in a LPP always occurs at only one corner point of the feasible region.
in a LPP always occurs at only one corner point of the feasible region.
Sol. False
44. In a LPP, the minimum value of the objective function 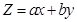 is always 0 if origin is one of the corner point of the feasible region.
is always 0 if origin is one of the corner point of the feasible region.
Sol. False
45. In a LPP, the maximum value of the objective function 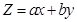 is always finite.
is always finite.
Sol. True