Linear Programming - Revision Notes

 CBSE Class 12 Mathematics

Chapter-12
Linear Programming

  • Linear Programming Problem: A linear programming problem is one that is concerned with finding the optimal value (maximum or minimum) of a linear function of several variables (called objective function) subject to the conditions that the variables are non-negative and satisfy a set of linear inequalities (called linear constraints). Variables are sometimes called decision variables and are non-negative.
  • A few important linear programming problems are:

         (i)       Diet problems

         (ii)      Manufacturing problems

         (iii)     Transportation problems

         (iv)     Allocation problems

  • The common region determined by all the constraints including the non-negative constraints 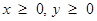 of a linear programming problem is called the feasible region (or solution region) for the problem.
  • Points within and on the boundary of the feasible region represent feasible solutions of the constraints. Any point outside the feasible region is an infeasible solution.
  • Any point in the feasible region that gives the optimal value (maximum or minimum) of the objective function is called an optimal solution.
  • The following Theorems are fundamental in solving linear programming problems:

Theorem 1 Let R be the feasible region (convex polygon) for a linear programming problem and let 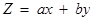 be the objective function. When Z has an optimal value (maximum or minimum), where the variables x and y are subject to constraints described by linear inequalities, this optimal value must occur at a corner point (vertex) of the feasible region.

Theorem 2 Let R be the feasible region for a linear programming problem, and let be the objective function.  If R is bounded, then the objective function Z has both a maximum and a minimum value on R and each of these occurs at a corner point (vertex) of R.

  • If the feasible region is unbounded, then a maximum or a minimum may not exist. However, if it exists, it must occur at a corner point of R.
  • Corner point method : For solving a linear programming problem. The method comprises of the following steps:

(i)     Find the feasible region of the linear programming problem and determine its corner points (vertices).

(ii)   Evaluate the objective function 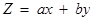at each corner point. Let M and m respectively be the largest and smallest values at these points.

(iii)     If the feasible region is bounded, M and m respectively are the maximum and minimum values of the objective function.

  • If the feasible region is unbounded, then,

(i)   M is the maximum value of the objective function, if the open half plane determined by 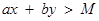has no point in common with the feasible region. Otherwise, the objective function has no maximum value.

(ii)   m is the minimum value of the objective function, if the open half plane determined by 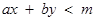 has no point in common with the feasible region. Otherwise, the objective function has no minimum value.

  • If two corner points of the feasible region are both optimal solutions of the same type, i.e., both produce the same maximum or minimum, then any point on the line segment joining these two points is also an optimal solution of the same type.