Matrices - Exemplar Solutions

 CBSE Class–12 Mathematics

NCERT Exemplar
Chapter - 3
Matrices - Short Answer Questions

---

1. Construct a matrix 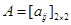whose elements aij are given by 

Sol.For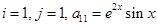 

For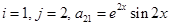 

For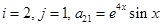 

For 

Thus,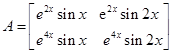 

2. If 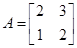, , , , 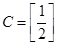then which of the sums A + B, B + C, C + D and B + D is defined?

Sol.Only B + D is defined since matrices of the same order can only be added.

3. Show that a matrix which is both symmetric and skew symmetric is a zero matrix.

Sol.Let A = [aij] be a matrix which is both symmetric and skew symmetric.

Since A is a skew symmetric matrix, so A′= –A.

Thus, for all , we have aij= – aji ....................(1)

Again, since A is a symmetric matrix, so A′= A.

Thus, for all , we have

aji =  aij  ..................... (2)

Therefore, from (1) and (2), we get

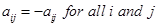
Or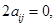 

i.e., for all i and j. Hence A is Zero matrix.

4. If 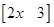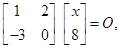find the value of x.

Sol.We have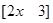 

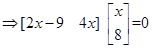
 =>[2x2−9x+32x]=[0]$=>[2x^2-9x+32x]=[0]$

=>[2x2+23x]=[0]$=>[2x^2+23x]=[0]$

=> 2x2 +23x = 0

Or 

5. If A is 3×3 invertible matrix, then show that for any scalar k(non-zero), kA is invertible and 

Sol.We have

Hence (kA) is inverse of 

---

Long Answer Questions

6. Express the matrix A as the sum of a symmetric and a skew symmetric matrix, where

Sol.We have

, then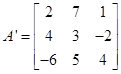 

Hence 

And A−A′2=12⎡⎣⎢037−30−7−770⎤⎦⎥$\frac{A-A^{\prime }}{2}=\frac{1}{2}\left[\begin{array}{ccc}0& -3& -7\\ 3& 0& 7\\ 7& -7& 0\end{array}\right]$ =⎡⎣⎢⎢03272−320−72−72720⎤⎦⎥⎥$=\left[\begin{array}{ccc}0& -\frac{3}{2}& -\frac{7}{2}\\ \frac{3}{2}& 0& \frac{7}{2}\\ \frac{7}{2}& -\frac{7}{2}& 0\end{array}\right]$

 

Therefore,

7. If 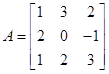, then show that A satisfies the equation

Sol.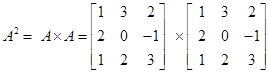

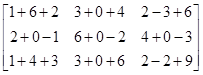
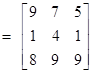
And 

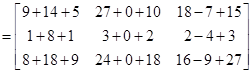
Now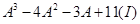 

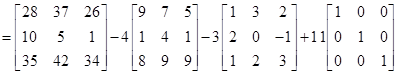
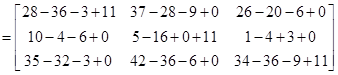
8. Let 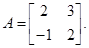Then show that Using this result calculate A5also.

Sol.We have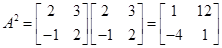 

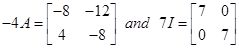
Therefore,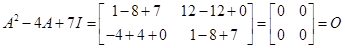 

Thus 

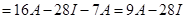
And so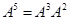 

= (9A – 28I) (4A – 7I)

= 36A2– 63A – 112A + 196I

= 36 (4A – 7I) – 175A + 196I

= – 31A – 56I

= 

---

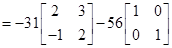
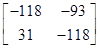
Objective Questions

Choose the correct answer from the given four options in s 9 to 12.

9. If A and B are square matrices of the same order, then (A + B) (A – B) is equal to

(A)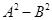 

(B)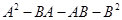 

(C) 

(D) 

Sol.(C) is correct answer. (A + B) (A – B) = A (A – B) + B (A – B)= A2– AB + BA – B2

10. If A = 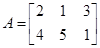and , then

(A) only AB is defined

(B) only BA is defined

(C) AB and BA both are defined

(D) AB and BA both are not defined.

Sol.(C) is correct answer. Let A = [aij]2×3 B = [bij]3×2. Both AB and BA are defined.

11. The matrix 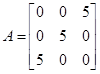is a

(A) scalar matrix

(B) diagonal matrix

(C) unit matrix

(D) square matrix

Sol.(D) is correct answer.

12. If A and B are symmetric matrices of the same order, then (AB′–BA′) is a

(A) Skew symmetric matrix

(B) Null matrix

(C) Symmetric matrix

(D) None of these

Sol.(A) is correct answer since

(AB′–BA′)′ = (AB′)′– (BA′)′

= (BA′– AB′)

= – (AB′–BA′)

Fill in the blanks in each of the s 13 to 15:

13. If A and B are two skew symmetric matrices of same order, then AB is symmetric matrix if ________.

Sol.AB = BA.

14. If A and B are matrices of same order, then (3A –2B)′is equal to ________.

Sol.3A′–2B′.

15. Addition of matrices is defined if order of the matrices is ________

Sol.Same.

State whether the statements in each of the s 16 to 19 is true or false:

16. If two matrices A and B are of the same order, then 2A + B = B + 2A.

Sol.True

17. Matrix subtraction is associative

Sol.False

18. For the non-singular matrix A, (A′)–1= (A–1)′.

Sol.True

19. AB = AC ⇒B = C for any three matrices of same order.

Sol.False