Matrices - Revision Notes

 CSBE Class 12 Mathematics

Chapter-3

Matrices

---

• A matrix is an ordered rectangular array of numbers, real or complex or functions.
• A matrix having m rows and n columns is called a matrix of order m × n.
• Column matrix: A matrix with one column is denoted by .
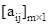• Row matrix: A matrix with one row is denoted by .
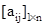• Square matrix: An m × n matrix is a square matrix if m = n.
• Diagonal matrix: A = 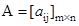 is a diagonal matrix if  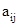=0, when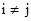 
• Scalar matrix: 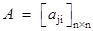 is a scalar matrix if  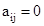  when  i ≠  j,  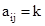   (k is some constant), when I=j.
• Identity matrix: 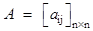 is an identity matrix, if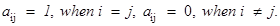 
• Zero matrix: A zero matrix has all its elements as zero.
• Equality of two matrices:   if (i) A and B are of same order, (ii) for all possible values of 
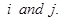
• Scalar multiplication:  

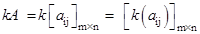
                                                Also       – A = (–1)A

• A – B = A + (–1) B

          A + B = B + A

          (A + B) + C = A + (B + C), where A = [aij],$\left[a_{ij}\right],$ B = [bij]$\left[b_{ij}\right]$ and C = [cij]$\left[c_{ij}\right]$ are of same order.

• k(A + B) = kA + kB, where A and B are of same order, k is constant.
• (k + l ) A = kA + lA, where k and l are constant.
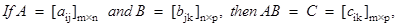• where

          

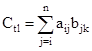
• (i)      A(BC) = (AB)C,

          (ii)     A(B + C) = AB + AC,

          (iii)    (A + B)C = AC + BC

• 
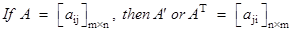
• (i) (A′)′ = A, ·   (ii) (kA)′ = kA′, ·   (iii) (A + B)′ = A′ + B′, ·   (iv) (AB)′ = B′A′
• Symmetric matrix: A is a symmetric matrix if A′ = A.
• Skew-aymmetric matrix: A is a skew symmetric matrix if A′ = –A.
• Any square matrix can be represented as the sum of a symmetric and a skew symmetric matrix. In fact, A = 12$\frac{1}{2}$(A + A') + 12$\frac{1}{2}$(A - A'), where 12$\frac{1}{2}$(A + A') is a symmetric matrix and 12$\frac{1}{2}$(A - A') is a skew-symmetric matrix.
• Equivalent matrices: Two matrices A and B are equivalent that is, A - B is A is obtained from the other by a sequence of elementary operations. Elementary operations of a matrix are as follows:

         (i)     Ri↔Rj${\mathrm{R}}_i\leftrightarrow {\mathrm{R}}_j$ or Ci→Cj${\mathrm{C}}_i\to {\mathrm{C}}_j$ (interchange rows or columns)

         (ii)    Ri→kRj${\mathrm{R}}_i\to k{\mathrm{R}}_j$ or Ci→kCj${\mathrm{C}}_i\to k{\mathrm{C}}_j$

         (iii)   Ri→Ri+kRj${\mathrm{R}}_i\to {\mathrm{R}}_i+k{\mathrm{R}}_j$ or Ci→Ci+kCj${\mathrm{C}}_i\to {\mathrm{C}}_i+k{\mathrm{C}}_j$

• If A and B are two square matrices such that AB = BA = I, then B is the inverse matrix of A and is denoted by 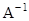and A is the inverse of  B.
• Inverse of a square matrix, if it exists, is unique.