Probability - Exemplar Solutions
CBSE Class–12 Mathematics
NCERT Exemplar
Chapter 13
Probability - Short Answer Questions
1. A and B are two candidates seeking admission in a college. The probability that A is selected is 0.7 and the probability that exactly one of them is selected is 0.6. Find the probability that B is selected.
Sol. Let p be the probability that B gets selected.
P(A is selected)=0.7,
P (Exactly one of A, B is selected) = 0.6
P (A is selected, B is not selected;B is selected, A is not selected) = 0.6
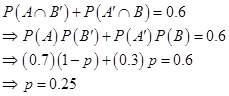
Thus, the probability that B gets selected is 0.25.
2. The probability of simultaneous occurrence of at least one of two events A and B is p. If the probability that exactly one of A, B occurs is q, then prove that 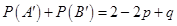 .
.
Sol. Since P (exactly one of A, B occurs) = q(given), we get
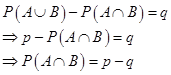
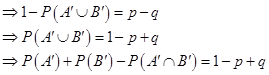
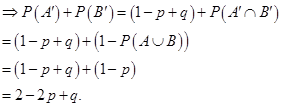
3. 10% of the bulbs produced in a factory are of red colour and 2% are red and defective. If one bulb is picked up at random, determine the probability of its being defective if it is red.
Sol. Let A and B be the events that the bulb is red and defective respectively.
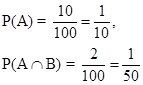
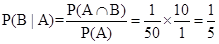
Thus, the probability of the picked up bulb of its being defective, if it is red, is 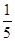 .
.
4. Two dice are thrown together. Let A be the event ‘getting 6 on the first die’ and B be the event ‘getting 2 on the second die’. Are the events A and B independent?
Sol. A = {(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
B = {(1, 2), (2, 2), (3, 2), (4, 2), (5, 2), (6, 2)}
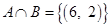
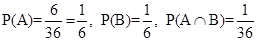
Events A and B will be independent if
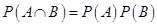
i.e., 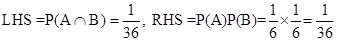
Here LHS=RHS
Hence, A and B are independent events.
5. A committee of 4 students is selected at random from a group consisting 8 boys and 4 girls. Given that there is at least one girl in the committee, calculate the probability that there are exactly 2 girls in the committee.
Sol. Let A denote the event that at least one girl will be chosen, and B the event that exactly 2 girls will be chosen. We require 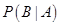 .
.
Since A denotes the event that at least one girl will be chosen, A’ denotes that no girl is chosen, i.e., 4 boys are chosen. Then
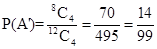
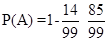
Now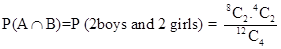
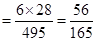
Thus 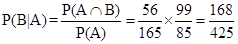
6. Three machines E1, E2, E3in a certain factory produce 50%, 25% and 25%, respectively, of the total daily output of electric tubes. It is known that 4% of the tubes produced one each of machines E1and E2are defective, and that 5% of those produced on E3are defective. If one tube is picked up at random from a day’s production, calculate the probability that it is defective.
Sol. Let D be the event that the picked up tube is defective.
Let 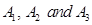 be the events that the tube is produced on machines
be the events that the tube is produced on machines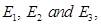 respectively.
respectively.
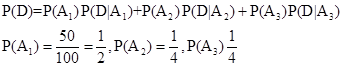
Also 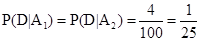
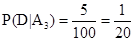
Putting these values in (1), we get
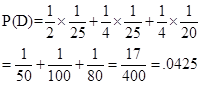
7. Find the probability that in 10 throws of a fair die a score which is a multiple of 3 will be obtained in at least 8 of the throws.
Sol. Here success is a score which is a multiple of 3 i.e., 3 or 6.
Therefore, 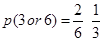
The probability of r success in 10 throws is given by
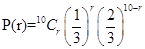
Now P (at least 8 successes) = P (8) + P (9) + P (10)
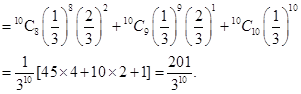
8. A discrete random variable X has the following probability distribution:

| X | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P(X) | C | 2C | 2C | 3C | C2 | 2C2 | 7C2+C |
Find the value of C. Also find the mean of the distribution.
Sol. Since 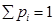 , we have
, we have
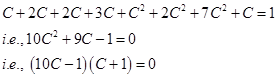
either (10C- 1)=0 or (C+1)=0
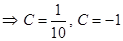 (C=-1 cannot be possible.probability cananot be negative)
(C=-1 cannot be possible.probability cananot be negative)
Therefore, the permissible value of 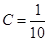 .
.
Mean = 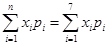
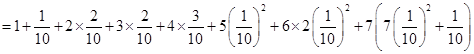
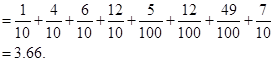
Long Answer
9. Four balls are to be drawn without replacement from a box containing 8 red and 4 white balls. If X denotes the number of red ball drawn, find the probability distribution of X.
Sol. Since 4 balls have to be drawn, therefore, X can take the values 0, 1, 2, 3, 4.
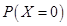 = P (no red ball) = P (4 white balls)
= P (no red ball) = P (4 white balls)
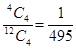
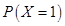 = P (1 red ball and 3 white balls)
= P (1 red ball and 3 white balls)
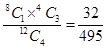
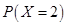 = P (2 red balls and 2 white balls)
= P (2 red balls and 2 white balls)
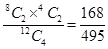
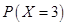 = P (3 red balls and 1 white ball)
= P (3 red balls and 1 white ball)
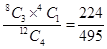
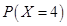 = P (4 red balls)
= P (4 red balls)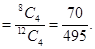
Thus, the following is the required probability distribution of X
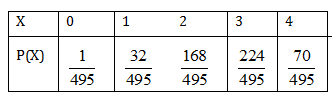
10. Determine variance and standard deviation of the number of heads in three tosses of a coin.
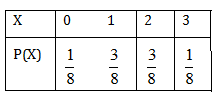
Sol. Let X denote the number of heads tossed. So, X can take the values 0, 1, 2, 3. When a coin is tossed three times, we get
Sample space S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
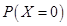 = P (no head) = P (TTT)
= P (no head) = P (TTT)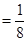
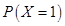 = P (one head) = P (HTT, THT, TTH)
= P (one head) = P (HTT, THT, TTH)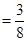
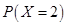 = P (two heads) = P (HHT, HTH, THH)
= P (two heads) = P (HHT, HTH, THH)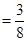
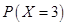 = P (three heads) = P (HHH)
= P (three heads) = P (HHH)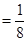
Thus the probability distribution of X is:
Variance of X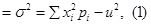
where μ is the mean of X given by
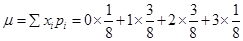
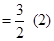
Now 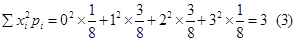
From (1), (2) and (3), we get
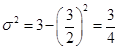
Standard deviation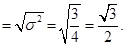
11. Refer to Example 6. Calculate the probability that the defective tube was produced on machine E1.
Sol. Now, we have to find 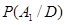 .
.
12. A car manufacturing factory has two plants, X and Y. Plant X manufactures 70% of cars and plant Y manufactures 30%. 80% of the cars at plant X and 90% of the cars at plant Y are rated of standard quality. A car is chosen at random and is found to be of standard quality. What is the probability that it has come from plant X?
Sol. Let E be the event that the car is of standard quality. Let 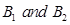 be the events that the car is manufactured in plants X and Y, respectively. Now
be the events that the car is manufactured in plants X and Y, respectively. Now
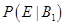 = Probability that a standard quality car is manufactured in plant X
= Probability that a standard quality car is manufactured in plant X
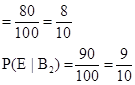
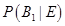 = Probability that a standard quality car has come from plant X
= Probability that a standard quality car has come from plant X
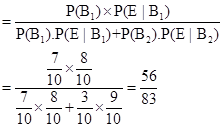
Hence the required probability is 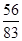 .
.
Choose the correct answer from the given four options in each of the Examples 13 to 17.
13. Let A and B be two events. If 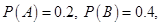
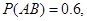 then
then 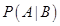 is equal to
is equal to
(A) 0.8
(B) 0.5
(C) 0.3
(D) 0
Sol. The correct answer is (D). From the given data 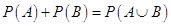 .
.
This shows that 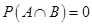 . Thus,
. Thus, 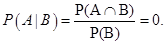
14. Let A and B be two events such that 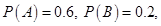 and
and 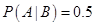 .
.
Then 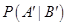 equals
equals
(A) 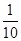
(B) 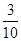
(C) 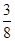
(D) 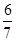
Sol. The correct answer is (C). 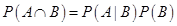
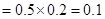
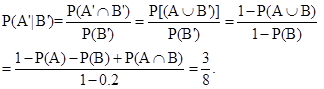
15. If A and B are independent events such that 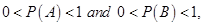 then which of the following is not correct?
then which of the following is not correct?
(A) 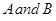 are mutually exclusive
are mutually exclusive
(B) 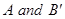 are independent
are independent
(C) 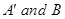 are independent
are independent
(D) 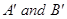 are independent
are independent
Sol. The correct answer is (A).
16. Let X be a discrete random variable. The probability distribution of X is given below:
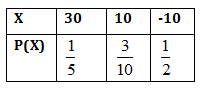
Then E (X) is equal to
(A) 6
(B) 4
(C) 3
(D) –5
Sol. The correct answer is (B).
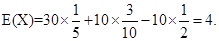
17. Let X be a discrete random variable assuming values 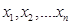 with probabilities
with probabilities 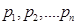 , respectively. Then variance of X is given by
, respectively. Then variance of X is given by
(A) 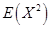
(B) 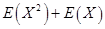
(C) 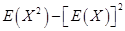
(D) 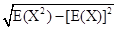
Sol. The correct answer is (C).
Fill in the blanks in Examples 18 and 19
18. If A and B are independent events such that 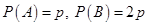 and P(Exactly one of A, B)
and P(Exactly one of A, B)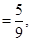 then p = _________________
then p = _________________
Sol. 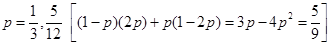
19. If 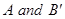 are independent events then
are independent events then 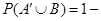 ________
________
Sol. 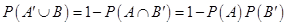
(since 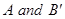 are independent).
are independent).
State whether each of the statement in Examples 20 to 22 is True or False
20. Let A and B be two independent events. Then 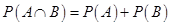 .
.
Sol. False, because 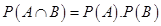 when events A and B are independent.
when events A and B are independent.
21. Three events A, B and C are said to be independent if 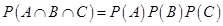 .
.
Sol. False. Reason is that A, B, C will be independent if they are pairwise independent and 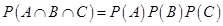 .
.
22. One of the condition of Bernoulli trials is that the trials are independent of each other.
Sol. True.