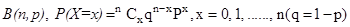Probability - Revision Notes

 CBSE Class 12 Mathematics

Chapter-13
Probability

---

• Sample Space: The set of all possible outcomes of a random experiment. It is denoted by the symbol S.
• Sample points: Elements of the sample space.
• Event: A subset of the sample space.
• Impossible Event: The empty set.
• Sure Event: The whole sample space.
• Complementary event or "not event": The set "S" or S - A.
• The event A or B: The set A ∪$\cup$ B.
• The event A and B: The set A ∩$\cap$ B.
• The event A but not B: A - B.
• Mutually exclusive events: A and B are mutually exclusive if A ∩$\cap$ B = ϕ$\varphi$.
• Exhaustive and Mutually exclusive events: Events E1, E2,........, En are mutually exclusive and exhaustive if E1∪$\cup$ E2 ∪$\cup$.......∪$\cup$ En = S and Ei ∩$\cap$ Ej = ϕ$\varphi$ for all i≠j$i\ne j$.
• Exiomatic approach to probability: To assign probabilities to various events, some axioms or rules have been described.

Let S be the sample space of a random experiment. The probability P is a real values function whose domain is the power set of S and range is the interval [0, 1] satisfying the following axioms:

(a) For any event E, P(E) ≥$\ge$ 0

(b) P(S) = 1

(c) If E and F are mutually exclusive event, then P(E ∪$\cup$ F) = P(E) + P(F)

If E1, E2, E3............ are n mutually exclusive events, then P(∪i=1nEi)=∑i=1nP(Ei)$\mathrm{P}\left(\underset{i=1}{\overset{n}{\cup }}{\mathrm{E}}_i\right)=\sum _{i=1}^n\mathrm{P}\left({\mathrm{E}}_i\right)$

• Probability of an event in terms of the probabilities of the same points (outcomes): Let S be the sample space containing n exhaustive outcomes W1,W2,W3,......Wn${\mathrm{W}}_1,{\mathrm{W}}_2,{\mathrm{W}}_3,......{\mathrm{W}}_n$ i.e., S = (W1,W2,W3,......Wn)$\left({\mathrm{W}}_1,{\mathrm{W}}_2,{\mathrm{W}}_3,......{\mathrm{W}}_n\right)$

Now from the axiomatic definition of the probability:

(a) 0 ≤$\le$ P(Wi) ≤$\le$ 1, for each Wi∈S${\mathrm{W}}_i\in \mathrm{S}$.

(b) P(W1) + P(W2) + .......+ P(W3) = P(S) = 1

(c) For any event A, P(A) = ∑P(Wi),$\sum \mathrm{P}\left({\mathrm{W}}_i\right),$ Wi∈A${\mathrm{W}}_i\in \mathrm{A}$

• Equally likely outcomes: All outcomes with equal probability.
• Classical definition of the probability of an event: For a finite sample space with equally likely outcome, probability of an event A.

P(A) = n(A)n(S)$\frac{n\left(\mathrm{A}\right)}{n\left(\mathrm{S}\right)}$ 

where n(A)$n\left(\mathrm{A}\right)$ = Number of elements in the set A. and n(S)$n\left(\mathrm{S}\right)$ = Number of elements in set S.

• If A is any event, then P(not A) = 1 - P(A) ⇒$\Rightarrow$ P(A¯¯¯¯)=1−P(A)$\mathrm{P}\left(\overline{\mathrm{A}}\right)=1-\mathrm{P}\left(\mathrm{A}\right)$ ⇒$\Rightarrow$ P(A′)=1−P(A)$\mathrm{P}\left({\mathrm{A}}^{\prime }\right)=1-\mathrm{P}\left(\mathrm{A}\right)$
• The conditional probability of an event E, given the occurrence of the event F is given by 
• 
• ·   
• ·   
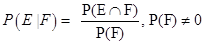
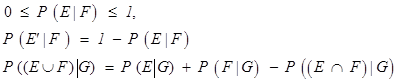
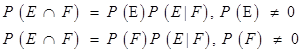
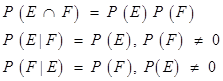
• Theorem of total probability:

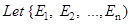 be a partition of a sample space and suppose that each of 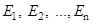has non zero probability.    Let A be any event associated with S, then

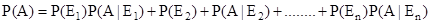
• Bayes' theorem: If 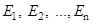are events which constitute a partition of sample space S, i.e. 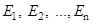are pairwise disjoint and 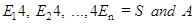be any event with non-zero probability, then,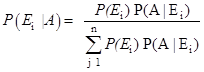 
• Random variable: A random variable is a real valued function whose domain is the sample space of a random experiment.
• Probability distribution: The probability distribution of a random variable X is the system of numbers

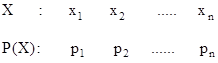
Where,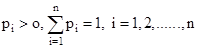 

• Mean of a probability distribution: Let X be a random variable whose possible values 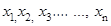occur with probabilities  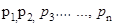 respectively.  The mean of X, denoted by  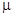is the number 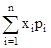. The mean of a random variable X is also called the expectation of X, denoted by E (X).
• Variance: Let X be a random variable whose possible values 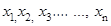occur with probabilities  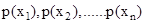  respectively. Let  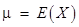be the mean of X. The variance of X, denoted by Var (X) or 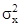 is defined as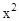 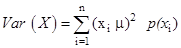  or equivalently  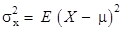. The non-negative number,  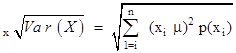is called the standard deviation of the random variable X.

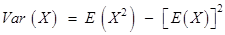
• Bernoulli Trials: Trials of a random experiment are called Bernoulli trials, if they satisfy the following conditions:

(i)   There should be a finite number of trials.

(ii)   The trials should be independent.

(iii)   Each trial has exactly two outcomes: success or failure.

(iv)   The probability of success remains the same in each trial.

For Binomial distribution