Relations and Functions - Revision Notes

 CBSE Class 12 Mathematics

Chapter-01
Relation and Function

---

TYPES OF RELATIONS:

• Empty Relation: It is the relation R in X given by R = ϕ⊂$\varphi \subset$ X×X$\mathrm{X}\times \mathrm{X}$.
• Universal Relation: It is the relation R in X given by R = X×X$\mathrm{X}\times \mathrm{X}$.
• Reflexive Relation: A relation R in a set A is called reflexive if (a, a) ∈ R for every a ∈ A.
• Symmetric Relation: A relation R in a set A is called symmetric if (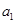, 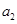) ∈ R implies that (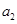, 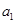) ∈ R, for all ,  ∈
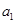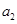• Transitive Relation: A relation R in a set A is called transitive if (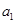, 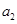) ∈ R, and (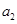, 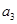) ∈ R together imply that all 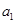, , 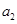 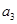∈ A.
• EQUIVALENCE RELATION : A relation R in a set A is said to be an equivalence relation if R is reflexive, symmetric and transitive.
• Equivalence Classes: Every arbitrary equivalence relation R in a set X divides X into mutually disjoint subsets (Ai) called partitions or subdivisions of X satisfying the following conditions:

All elements of Ai are related to each other for all i.
No element of Ai is related to any element of Aj whenever i ≠ j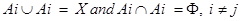 

·   . These subsets (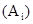) are called equivalence classes.

·   For an equivalence relation in a set X, the equivalence class containing a ∈ X, denoted by [a], is the subset of X containing all elements b related to a.

**Function: A relation f: A B is said to be a function if every clement of A is correlated to a

Unique element in B.

*A is domain

* B is codomain

• A function f$f$ : X →$\to$ Y is one-one (or injective), if f(x1)=f(x2)$f\left(x_1\right)=f\left(x_2\right)$ ⇒$\Rightarrow$ x1=x2,$x_1=x_2,$ ∀$\mathrm{\forall }$ x1,x2∈X$x_1,x_2\in \mathrm{X}$.
• A function f$f$ : X →$\to$ Y is onto (or surjective), if y∈Y,$y\in \mathrm{Y},$ ∃x∈X$\mathrm{\exists }x\in \mathrm{X}$ such that f(x)=y.$f\left(x\right)=y.$
•  A function f$f$ : X →$\to$ Y is one-one-onto (or bijective), if f$f$ is both one-one and onto.
• The composition of function f$f$ : A →$\to$ B and g$g$ : B →$\to$ C is the function gof:A→C$gof:\mathrm{A}\to \mathrm{C}$ given by gof(x)=g(f(x)),$gof\left(x\right)=g\left(f\left(x\right)\right),$ ∀x∈A.$\mathrm{\forall }x\in \mathrm{A}.$
• A function f$f$ : X →$\to$ Y is invertible, if ∃g:Y→X$\mathrm{\exists }g:\mathrm{Y}\to \mathrm{X}$ such that  gof=Ix$gof={\mathrm{I}}_x$ and fog=Iy.$fog={\mathrm{I}}_y.$
• A function f$f$ : X →$\to$ Y is invertible, if and only if f$f$ is one-one and onto.
• Given a finite set X, a function f$f$ : X →$\to$ X is one-one (respectively onto) if and only if f$f$ is onto (respectively one-one). This is the characteristics property of a finite set. This is not true for infinite set.
• A binary function * on A is a function * from A x A to A.
• An element e∈X$e\in \mathrm{X}$ is the identity element for binary operation * : X×X→X$\mathrm{X}\times \mathrm{X}\to \mathrm{X}$, if a∗e=a=e∗a$a\ast e=a=e\ast a$ ∀a∈X.$\mathrm{\forall }a\in \mathrm{X}.$
• An element e∈X$e\in \mathrm{X}$ is invertibel for binary operation * : X×X→X$\mathrm{X}\times \mathrm{X}\to \mathrm{X}$ if there exists b∈X$b\in \mathrm{X}$ such that a∗b∗e∗b∗a,$a\ast b\ast e\ast b\ast a,$ where e$e$ is the binary identity for the binary operation *. The element b$b$ is called the inverse of a$a$ and is denoted by a−1$a^{-1}$.
• An operation * on X is commutative, if a∗b=b∗a,$a\ast b=b\ast a,$ ∀a,b$\mathrm{\forall }a,b$ in X.
• An operation * on X is associative, if (a∗b)∗c=a∗(b∗c),$(a\ast b)\ast c=a\ast (b\ast c),$ ∀a,b,c$\mathrm{\forall }a,b,c$ in X.