Relations and Functions - Exemplar Solutions
CBSE Class–12 Mathematics
NCERT Exemplar
Chapter - 1
Relations and Functions - Short Answer Questions
1. Let A = {0, 1, 2, 3} and define a relation R on A as follows:
R = {(0, 0), (0, 1), (0, 3), (1, 0), (1, 1), (2, 2), (3, 0), (3, 3)}.
Is R reflexive? symmetric? transitive?
Sol. R is reflexive and symmetric, but not transitive since for (1, 0) ∈ R and (0, 3) ∈ R whereas (1, 3) ∉ R.
2. For the set A = {1, 2, 3}, define a relation R in the set A as follows:
R = {(1, 1), (2, 2), (3, 3), (1, 3)}.
Write the ordered pairs to be added to R to make it the smallest equivalence relation.
Sol. (3, 1) is the single ordered pair which needs to be added to R to make it the smallest equivalence relation.
3. Let R be the equivalence relation in the set Z of integers given by R = {(a, b) : 2 divides a– b}. Write the equivalence class [0].
Sol. [0] = {0, ± 2, ± 4, ± 6, ...}
4. Let the function 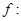 R → R be defined by
R → R be defined by  Then, show that
Then, show that  is one-one.
is one-one.
Sol. For any two elements  ∈ R such that
∈ R such that 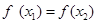 , we have
, we have
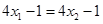

Hence  is one-one.
is one-one.
5. If  = {(5, 2), (6, 3)},
= {(5, 2), (6, 3)},  = {(2, 5), (3, 6)}, write
= {(2, 5), (3, 6)}, write  o
o .
.
Sol.  o
o = {(2, 2), (3, 3)}
= {(2, 2), (3, 3)}
6. Let 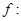 R → R be the function defined by
R → R be the function defined by  Then write
Then write 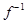
Sol. Given that 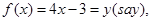 then
then


Hence 
7. Is the binary operation * defined on Z (set of integer) by 
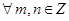 commutative?
commutative?
Sol. No. Since for  while
while 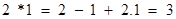 so that 1*2 ≠2 *1.
so that 1*2 ≠2 *1.
8. If  = {(5, 2), (6, 3)} and
= {(5, 2), (6, 3)} and  = {(2, 5), (3, 6)}, write the range of
= {(2, 5), (3, 6)}, write the range of  and
and  .
.
Sol. The range of  = {2, 3} and the range of
= {2, 3} and the range of  = {5, 6}.
= {5, 6}.
9. If A = {1, 2, 3} and  ,
,  are relations corresponding to the subset of
are relations corresponding to the subset of 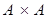 indicated against them, which of
indicated against them, which of  ,
,  is a function? Why?
is a function? Why?
 = {(1, 3), (2, 3), (3, 2)}
= {(1, 3), (2, 3), (3, 2)}
 = {(1, 2), (1, 3), (3, 1)}
= {(1, 2), (1, 3), (3, 1)}
Sol.  is a function since each element of A in the first place in the ordered pairs is related to only one element of A in the second place while g is not a function because 1 is related to more than one element of A, namely, 2 and 3.
is a function since each element of A in the first place in the ordered pairs is related to only one element of A in the second place while g is not a function because 1 is related to more than one element of A, namely, 2 and 3.
10. If A = {a, b, c, d} and  = {a, b), (b, d), (c, a), (d, c)}, show that
= {a, b), (b, d), (c, a), (d, c)}, show that  is one-one from A onto A. Find
is one-one from A onto A. Find 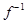
Sol.  is one-one since each element of A is assigned to distinct element of the set A. Also,
is one-one since each element of A is assigned to distinct element of the set A. Also,  is onto since
is onto since  (A) = A. Moreover,
(A) = A. Moreover, 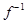 = {(b, a), (d, b), (a, c), (c, d)}.
= {(b, a), (d, b), (a, c), (c, d)}.
11. In the set N of natural numbers, define the binary operation *by 
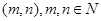 . Is the operation * commutative and associative?
. Is the operation * commutative and associative?
Sol. The operation is clearly commutative since
m*n= g.c.d (m, n) = g.c.d(n, m) = n * m 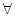 m, n
m, n 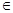 N.
N.
It is also associative because for l, m, n 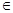 N, we have
N, we have
l *(m*n) = g. c. d (l, g.c.d (m, n))
= g.c.d. (g. c. d(l, m), n)
= (l*m) *n.
12. In the set of natural numbers N, define a relation R as follows:
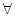 n, m
n, m 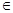 N, nRm if on division by 5 each of the integers n and m leaves the remainder less than 5, i.e. one of the numbers 0, 1, 2, 3 and 4. Show that R is equivalence relation. Also, obtain the pairwise disjoint subsets determined by R.
N, nRm if on division by 5 each of the integers n and m leaves the remainder less than 5, i.e. one of the numbers 0, 1, 2, 3 and 4. Show that R is equivalence relation. Also, obtain the pairwise disjoint subsets determined by R.
Sol. R is reflexive since for each a 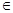 N, aRa. R is symmetric since if aRb, then bRa for a, b
N, aRa. R is symmetric since if aRb, then bRa for a, b 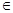 N. Also, R is transitive since for a, b, c
N. Also, R is transitive since for a, b, c 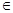 N, if aRb and bRc, then aRc.
N, if aRb and bRc, then aRc.
Hence R is an equivalence relation in N which will partition the set N into the pairwise disjoint subsets. The equivalent classes are as mentioned below:
A0= {5, 10, 15, 20 ...}
A1= {1, 6, 11, 16, 21 ...}
A2= {2, 7, 12, 17, 22, ...}
A3= {3, 8, 13, 18, 23, ...}
A4= {4, 9, 14, 19, 24, ...}
It is evident that the above five sets are pairwise disjoint and

13. Show that the function 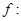 R → R defined by
R → R defined by 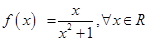 , is neither one-one nor onto.
, is neither one-one nor onto.
Sol. For x1, x2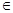 R, consider
R, consider
 (x1) =
(x1) =  (x2)
(x2)
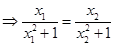
⇒ 
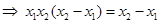
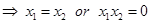
We note that there are point, 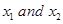 with
with 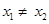 and
and  for instance, if we take
for instance, if we take  and
and 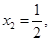 then we have
then we have  and
and  but
but 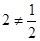 . Hence
. Hence  is not one-one. Also,
is not one-one. Also,  is not onto for if so then for
is not onto for if so then for  such that
such that  (x) = 1 which gives
(x) = 1 which gives 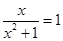 . But there is no such x in the domain R, since the equation
. But there is no such x in the domain R, since the equation  does not give any real value of x.
does not give any real value of x.
14. Let  ,
,  : R → R be two functions defined as
: R → R be two functions defined as 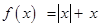 and
and 
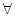 x
x 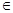 R. Then, find
R. Then, find 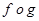 and
and  .
.
Sol. Here 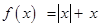 which can be redefined as
which can be redefined as
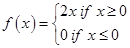
Similarly, the function  defined by
defined by 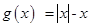 may be redefined as
may be redefined as
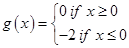
Therefore,  gets defined as:
gets defined as:
For x ≥0, ( ) (x) =
) (x) =  (
( (x) =
(x) =  (2x) = 0
(2x) = 0
and for x <0, ( ) (x) =
) (x) =  (
( (x) =
(x) =  (0) = 0.
(0) = 0.
Consequently, we have ( ) (x) = 0,
) (x) = 0,  x
x 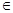 R.
R.
Similarly, 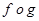 gets defined as:
gets defined as:
For x ≥0, (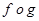 ) (x) =
) (x) =  (
( (x) =
(x) =  (0) = 0,
(0) = 0,
and for x <0, (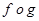 ) (x) =
) (x) =  (
( (x)) =
(x)) =  (–2 x) = – 4x.
(–2 x) = – 4x.
i.e. 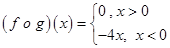
15. Let R be the set of real numbers and  be the function defined by
be the function defined by  (x) = 4x+ 5. Show that
(x) = 4x+ 5. Show that  is invertible and find
is invertible and find 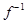 .
.
Sol. Here the function  is defined as
is defined as  (say). Then
(say). Then
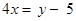 or
or 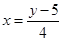
This leads to a function  defined as
defined as

Therefore,  =
=

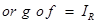
Similarly, (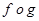 ) (y) =
) (y) =  (
( (y))
(y))
= 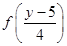
= 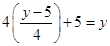
or 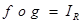 .
.
Hence  is invertible and
is invertible and  which is given by
which is given by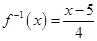
16. Let * be a binary operation defined on Q. Find which of the following binary operations are associative.
(i) a *b= a– b for a, b 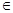 Q.
Q.
(ii) 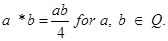
(iii) a *b= a– b+ ab for a, b 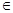 Q.
Q.
(iv) 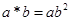 for a, b
for a, b 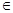 Q.
Q.
Sol. (i) * is not associative for if we take a= 1, b= 2 and c= 3, then
(a*b) *c= (1 *2) * 3 = (1 – 2) * 3 = – 1 – 3 = – 4 and
a *(b*c) = 1 *(2 *3) = 1 *(2 – 3) = 1 – (– 1) = 2.
Thus (a*b) *c ≠ a*(b*c) and hence * is not associative.
(ii) * is associative since Q is associative with respect to multiplication.
(iii) * is not associative for if we take a= 2, b= 3 and c = 4, then
(a*b) *c= (2 *3) * 4 = (2 – 3 + 6) *4 = 5*4 = 5 – 4 + 20 = 21, and
a*(b*c) = 2 *(3*4) = 2*(3 – 4 + 12) = 2 *11 = 2 – 11 + 22 = 13
Thus (a*b) * c ≠ a*(b*c) and hence * is not associative.
(iv) * is not associative for if we take a= 1, b= 2 and c= 3, then (a*b) * c=(1 * 2) * 3 = 4 * 3 = 4 × 9 = 36 and a*(b*c) = 1 * (2 * 3) = 1*18 =
Thus (a * b) * c ≠ a * (b * c) and hence*is not associative.
Choose the correct answer from the given four options in each of the Examples 17 to 25.
17. Let R be a relation on the set N of natural numbers defined by nRm if n divides m. Then R is
(A) Reflexive and symmetric
(B) Transitive and symmetric
(C) Equivalence
(D) Reflexive, transitive but not symmetric
Sol. The correct choice is (D).
Since n divides n, 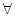 n
n  N, R is reflexive. R is not symmetric since for 3, 6
N, R is reflexive. R is not symmetric since for 3, 6  N, 3 R 6 ≠6 R 3. R is transitive since for n, m, r whenever n/m and m/r ⇒ n/r, i.e., n divides m and m divides r, then n will divide r.
N, 3 R 6 ≠6 R 3. R is transitive since for n, m, r whenever n/m and m/r ⇒ n/r, i.e., n divides m and m divides r, then n will divide r.
18. Let L denote the set of all straight lines in a plane. Let a relation R be defined by lRm if and only if l is perpendicular to m  l, m
l, m  L. Then R is
L. Then R is
(A) reflexive
(B) symmetric
(C) transitive
(D) none of these
Sol. The correct choice is (B).
19. Let N be the set of natural numbers and the function  : N → N be defined by
: N → N be defined by  (n) = 2n+ 3
(n) = 2n+ 3 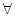 n
n 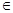 N. Then
N. Then  is
is
(A) surjective
(B) injective
(C) bijective
(D) none of these
Sol. (B) is the correct option.
20. Set A has 3 elements and the set B has 4 elements. Then the number of injective mappings that can be defined from A to B is
(A) 144
(B) 12
(C) 24
(D) 64
Sol. The correct choice is (C). The total number of injective mappings from the set containing 3 elements into the set containing 4 elements is 
21. Let  : R → R be defined by
: R → R be defined by  (x) = sin x and
(x) = sin x and  : R → R be defined by
: R → R be defined by , then
, then 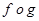 is
is
(A) 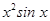
(B) (sin x)2
(C) 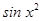
(D)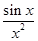
Sol. (C) is the correct choice.
22. Let  : R → R be defined by
: R → R be defined by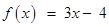 . Then
. Then  –1(x) is given by
–1(x) is given by
(A)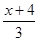
(B) 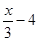
(C) 
(D) None of these
Sol. (A) is the correct choice.
23. Let  : R → R be defined by
: R → R be defined by  (x) = x2 + 1. Then, pre-images of 17 and – 3, respectively, are
(x) = x2 + 1. Then, pre-images of 17 and – 3, respectively, are
(A) 
(B) 
(C) 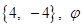
(D) {4, – 4, {2, – 2}
Sol. (C) is the correct choice since for  or
or  ⇒ x= ± 4 or f –1( 17) = {4, – 4} and for
⇒ x= ± 4 or f –1( 17) = {4, – 4} and for 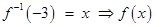
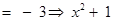
 and hence
and hence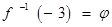 .
.
24. For real numbers x and y, define xRy if and only if 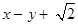 is an irrational number. Then the relation R is
is an irrational number. Then the relation R is
(A) reflexive
(B) symmetric
(C) transitive
(D) none of these
Sol. (A) is the correct choice.
Fill in the blanks in each of the Examples 25 to 30.
25. Consider the set A = {1, 2, 3} and R be the smallest equivalence relation on A, then R = ________
Sol. R = {(1, 1), (2, 2), (3, 3)}.
26. The domain of the function  : R → R defined by
: R → R defined by 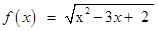 is ________.
is ________.
Sol. Here x2– 3x+ 2 ≥0
⇒ (x– 1) (x– 2) ≥0
⇒ x≤1 or x ≥2
Hence the domain of 
27. Consider the set A containing n elements. Then, the total number of injective functions from A onto itself is ________.
Sol. n!
28. Let Z be the set of integers and R be the relation defined in Z such that aRb if a– b is divisible by 3. Then R partitions the set Z into ________ pairwise disjoint subsets.
Sol. Three.
29. Let R be the set of real numbers and *be the binary operation defined on R as a * b= a + b– ab 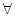 a, b
a, b 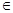 R. Then, the identity element with respect to the binary operation * is _______.
R. Then, the identity element with respect to the binary operation * is _______.
Sol. 0 is the identity element with respect to the binary operation *.
State True or False for the statements in each of the Examples 30 to 34.
30. Consider the set A = {1, 2, 3} and the relation R = {(1, 2), (1, 3)}. R is a transitive relation.
Sol. True.
31. Let A be a finite set. Then, each injective function from A into itself is not surjective.
Sol. False.
32. For sets A, B and C, let  : A →B,
: A →B,  : B →C be functions such that
: B →C be functions such that  is injective. Then both
is injective. Then both  and
and  are injective functions.
are injective functions.
Sol. False.
33. For sets A, B and C, let  : A →B,
: A →B,  : B →C be functions such that
: B →C be functions such that  is surjective. Then
is surjective. Then  is surjective.
is surjective.
Sol. True.
34. Let N be the set of natural numbers. Then, the binary operation * in N defined as 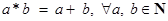 has identity element.
has identity element.
Sol. False.