Application of Derivatives - Revision Notes

 CBSE Class 12 Mathematics

Chapter-6
Application of Derivatives

---

• If a quantity y varies with another quantity x, satisfying some rule y = f(x), then 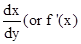represents the rate of change of y with respect to x and 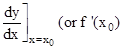represents the  rate of change of y with respect to x at x = xo.
• If two variables x and y are varying with respect to another variable t, i.e., if 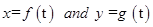  then by Chain Rule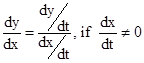
  
• A function f is said to be increasing on an interval (a,  b) if x1<x2$x_1<x_2$ in (a,b)⇒f(x1)<f(x2)$\left(a,b\right)\Rightarrow f\left(x_1\right)<f\left(x_2\right)$ for all x1,x2∈(a,b).$x_1,x_2\in \left(a,b\right).$  Alternatively, if  f′(x)>0$f^{\prime }\left(x\right)>0$ for each x$x$ in, then f(x) is an increasing funciton on (a, b).
• A function f is said to be decreasing on an interval (a,  b) if x1<x2$x_1<x_2$ in (a,b)⇒f(x1)>f(x2)$\left(a,b\right)\Rightarrow f\left(x_1\right)>f\left(x_2\right)$ for all x1,x2∈(a,b).$x_1,x_2\in \left(a,b\right).$  Alternatively, if  f′(x)>0$f^{\prime }\left(x\right)>0$ for each x$x$ in, then f(x) is an decreasing funciton on (a, b).
• The equation of the tangent at 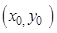   to the curve y =  f (x) is given by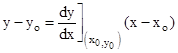
  
• If 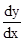  does not exist at the point 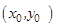, then the tangent at this point is parallel to the y-axis and its equation is.
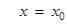• If tangent to a curve 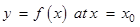 is parallel to x-axis, then 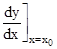= 0
• Equation of the normal to the curve y = f (x) at a point 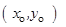is given by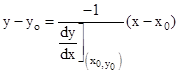 
• If 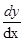 at the point 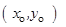is zero, then equation of the normal is x=x0$x=x_0$.
• If 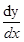 at the point  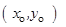does not exist, then the normal is parallel to x-axis and its equation is.
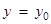• Let y = f (x), ∆x be a small increment in x and ∆y be the increment in y corresponding to the increment in x, i.e., ∆y = f (x + ∆x) –  f (x). Then dy$dy$ given by dy=f′(x)dx$dy=f^{\prime }\left(x\right)dx$ or dy=(dydx)dx$dy=\left(\frac{dy}{dx}\right)dx$ is a good approximation of ∆y when  dx x = ∆  is relatively small and we denote it by dy ≈ ∆y.
• A point c in the domain of a function f at which either f ′(c) = 0 or f is not differentiable is called a critical point of f.
• First Derivative Test : Let f  be a function defined on an open interval I. Let f   be continuous at a critical point c in I. Then,

(i) If f ′(x) changes sign from positive to negative as x increases through c, i.e., if f ′(x) > 0 at every point sufficiently close to and to the left of c, and f ′(x) < 0 at every point sufficiently close to and to the right of c, then c is a point of local maxima.

(ii) If f ′(x) changes sign from negative to positive as x increases through c, i.e., if f ′(x) < 0 at every point sufficiently close to and to the left of c, and f ′(x) > 0 at every point sufficiently close to and to the right of c, then c is a point of local minima.

(iii) If f ′(x) does not change sign as x increases through c, then c is neither a point of local maxima nor a point of local minima. In fact, such a point is called point of inflexion.

• Second Derivative Test : Let f be a function defined on an interval I and c ∈ I. Let f   be twice differentiable at c. Then,

(i) x = c is a point of local maxima if f ′(c) = 0 and f ″(c) < 0
The values f (c) is local maximum value of   f.

(ii) x = c is a point of local minima if f ′(c) = 0 and f ″(c) > 0
In this case, f (c) is local minimum value of f.

(iii) The test fails if f ′(c) = 0 and f ″(c) = 0.
In this case, we go back to the first derivative test and find whether c is a point of maxima, minima or a point of inflexion.

• Working rule for finding absolute maxima and/or absolute minima

Step 1: Find all critical points of f in the interval, i.e., find points x where either f ′(x) = 0 or f is not differentiable.

Step 2: Take the end points of the interval.

Step 3: At all these points (listed in Step 1 and 2), calculate the values of f.

Step 4: Identify the maximum and minimum values of f out of the values calculated in Step 3.

This maximum value will be the absolute maximum value of f and the minimum value will be the absolute minimum value of f .