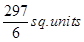Application of Integrals - Exemplar Solutions

 CBSE Class–12 Mathematics

NCERT Exemplar
Chapter - 8
APPLICATION OF INTEGRALS - Short Answer Questions

---

1. Find the area of the curve 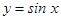between 0 and .

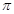Sol.We have

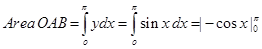
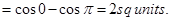
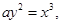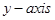2. Find the area of the region bounded by the curve the and the lines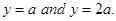 

Sol.We have

AreaBMNC=∫a2axdy=∫a2aa1/3y2/3dy$AreaBMNC=\underset{a}{\overset{2a}{\int }}xdy=\underset{a}{\overset{2a}{\int }}{a}^{1/3}{y}^{2/3}dy$

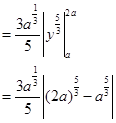
3. Find the area of the region bounded by the parabola 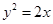and the straight line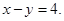 

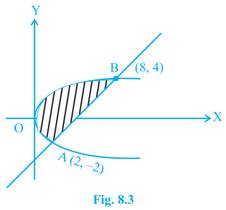
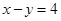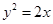Sol.The intersecting points of the given curves are obtained by solving the equations and for .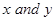
We have 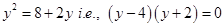which gives .
Thus, the points of intersection are 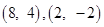. Hence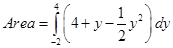

4. Find the area of region bounded by the parabolas .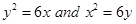

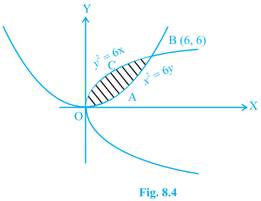
Sol.The intersecting points of the given parabolas are obtained by solving these equations for which are O (0,0) and B (6,6). Hence

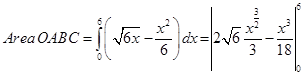
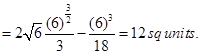
5. Find the area enclosed by the curve .

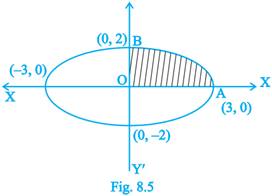
Sol.Eliminating as follows:
we obtain 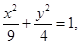which is the equation of an ellipse.
From Fig. 8.5, we get the required area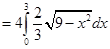 

 

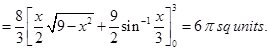
Long Answer Questions

---

6. Find the area of the region included between the parabola and the line .

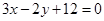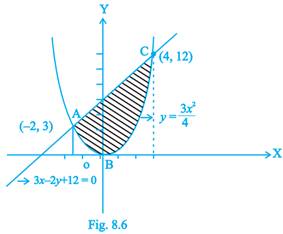
Sol.Solving the equations of the given curves and we get 

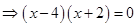
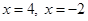which give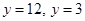 

From Fig. 8.6, the required area = area of ABC

7. Find the area of the region bounded by the curves 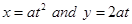between the ordinate coresponding to .

Sol.Given that 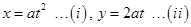putting the value of 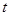in we get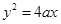 
Putting in (i), we get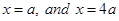 
Required area = 2 area of ABCD =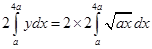 

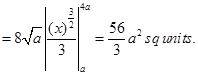
8. Find the area of the region above the 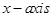, included between the parabola 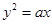and the circle .

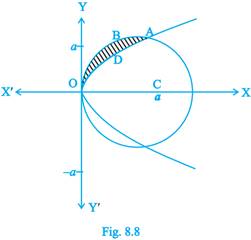
Sol.Solving the given equations of curves, we have

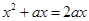
Or 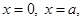which give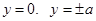

From Fig. 8.8 area ODAB = 
Let 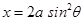. Then =.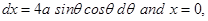
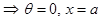
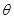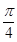Again, 

Further more,

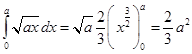
Thus the required area=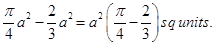 

Note: , we can also apply some special integral formula as shown below:

∫0a2ax−x2−a2+a2−−−−−−−−−−−−−−−√dx=∫0aa2−(x−a)2−−−−−−−−−−−√dx$\underset{0}{\overset{a}{\int }}\sqrt{2ax-x^2-a^2+a^2}dx=\underset{0}{\overset{a}{\int }}\sqrt{a^2-{(x-a)}^2}dx$

=[(x−a)22ax−x2−−−−−−−√+a22sin−1(x−a)a]a0$={\left[\frac{(x-a)}{2}\sqrt{2ax-x^2}+\frac{a^2}{2}{\sin }^{-1}\frac{(x-a)}{a}\right]}_0^a$=a22π2=a2π4$=\frac{a^2}{2}\frac{\pi }{2}=\frac{a^2\pi }{4}$

 

9. Find the area of a minor segment of the circle cut off by the line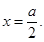 

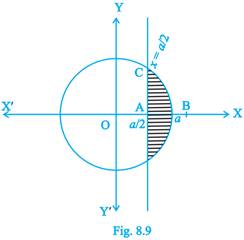
Sol.Solving the equation and 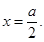, we obtain their points of intersection which are 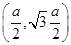and .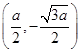

Hence, from Fig. 8.9, we get

Required Area =

 

Objective Questions

---

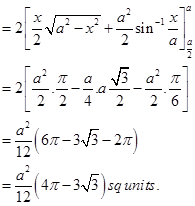
Choose the correct anwer from the given four options in each of the Examples 10 to 12.

10. The area enclosed by the circle is equal to

(A)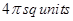 

(B)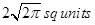 

(C)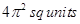 

(D) 

Sol.Correct answer is (D); since Area 

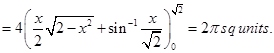
11. The area enclosed by the ellipse 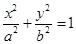is equal to

(A) 

(B)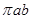 

(C) 

(D)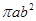 

Sol.Correct answer is (B); since Area 

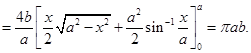
12. The area of the region bounded by the curve and the line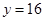 

(A)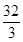 

(B)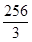 

(C) 

(D)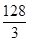 

Sol.Correct answer is (B); since Area =2∫016y√dy=43(y3/2)160=43(163/2−0)=43(64)=2563$2\underset{0}{\overset{16}{\int }}\sqrt{y}dy=\frac{4}{3}{\left(y^{3/2}\right)}_0^{16}=\frac{4}{3}({16}^{3/2}-0)=\frac{4}{3}(64)=\frac{256}{3}$

Fill in the blanks in each of the Examples 13 to 14.

13. The area of the region bounded by the curve 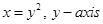and the line 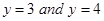is __________.

Sol.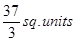

Area = ∫34xdy$\underset{3}{\overset{4}{\int }}xdy$

=∫34y2dy=(y33)43=64−273=373sq.units$\underset{3}{\overset{4}{\int }}{y}^{2}dy={\left(\frac{y^3}{3}\right)}_3^4=\frac{64-27}{3}=\frac{37}{3}sq.units$

 

14. The area of the region bounded by the curve 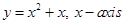and the line 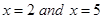is equal to _______________ .

Sol.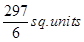

Area = ∫25ydx=∫25x2+xdx$\underset{2}{\overset{5}{\int }}ydx=\underset{2}{\overset{5}{\int }}{x}^2+xdx$

=(x33+x22)52=(1253+252−83−42)$={\left(\frac{x^3}{3}+\frac{x^2}{2}\right)}_2^5=\left(\frac{125}{3}+\frac{25}{2}-\frac{8}{3}-\frac{4}{2}\right)$

=