Application of Integrals - Revision Notes

 CBSE Class 12 Mathematics

Chapter-8
Application of Integrals

---

• Elementary area: The area is called elementary area which is located at any arbitary position within the region which is specified by some value of x$x$ between a$a$ and b.$b.$
   
• The area of the region bounded by the curve y = f (x), x-axis and the lines x = a and x = b (b > a) is given by the formula: 
   
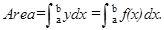
• The area of the region bounded by the curve x=θ(y)$x=\theta \left(y\right)$, y-axis and the lines y = c, y = d is given by the formula: 
   
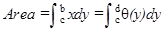
• The area of the region enclosed between two curves y = f (x), y = g (x) and the lines x = a, x = b is given by the formula, Area = ∫ab[f(x)−g(x)]dx$\underset{a}{\overset{b}{\int }}\left[f\left(x\right)-g\left(x\right)\right]dx$, where f(x)≥g(x)$f\left(x\right)\ge g\left(x\right)$ in [a, b].
   
• If f(x)≥g(x)$f\left(x\right)\ge g\left(x\right)$ in [a, c] and f(x)≤g(x)$f\left(x\right)\le g\left(x\right)$ in [c, b], a<c<b,$a<c<b,$ then we write the areas as : Area = ∫ab[f(x)−g(x)]dx+∫cb[g(x)−f(x)]dx$\underset{a}{\overset{b}{\int }}\left[f\left(x\right)-g\left(x\right)\right]dx+\underset{c}{\overset{b}{\int }}\left[g\left(x\right)-f\left(x\right)\right]dx$.