Application of Integrals - Test Papers

             CBSE Test Paper 01

Chapter 8 Application of Integrals

---

1. The area bounded by the curves y2=20x$y^2=20x$ and x2=16y$x^2=16y$ is equal to

   1. 3203 sq. units$\frac{320}{3}sq.units$
   2. 80π sq. units$80\pi sq.units$
   3. none of these
   4. 100π sq. units$100\pi sq.units$

2. The area of the region bounded by the parabola ( y - 2)2 = x - 1, the tangent to the parabola at the point ( 2 , 3 ) and the x – axis is equal to 

   1. none of these
   2. 6 sq. units
   3. 9 sq. units
   4. 12 sq. units

3. The area bounded by the curves y=x−−√,$y=\sqrt{x},$ 2y + 3 = xand the x – axis in the first quadrant is 

   1. 36
   2. 18
   3. 9
   4. none of these

4. If the area cut off from a parabola by any double ordinate is k times the corresponding rectangle contained by that double ordinate and its distance from the vertex, then k is equal to 

   1. 23$\frac{2}{3}$
   2. 3
   3. 13$\frac{1}{3}$
   4. 32$\frac{3}{2}$

5. The area bounded by the curves y = cos x and y = sin x between the ordinates x = 0 and x=π2$x=\frac{\pi }{2}$is equal to 

   1. 2(2–√+1)$2(\sqrt{2}+1)$ sq. units
   2. 2(2–√−1)$2(\sqrt{2}-1)$ sq. units
   3. (42–√−1)$\left(4\sqrt{2}-1\right)$ sq. units
   4. (42–√+1)$\left(4\sqrt{2}+1\right)$ sq. units

6. The area of the bounded by the lines y = 2, x = 1, x = a and the curve y = f(x), which cuts the last two lines above the first line for all a≥1$a\ge 1$, is equal to 23[(2a)3/2−3a+3−22–√]$\frac{2}{3}\left[(2a{)}^{3/2}-3a+3-2\sqrt{2}\right]$. Find f(x) 

7. Let f(x) be a continuous function such that the area bounded by the curve y=f(x), x-axis and the lines x=0 and x=a is a22+a2sin a+π2 cos a,$\frac{a^2}{2}+\frac{a}{2}sina+\frac{\pi }{2}cosa,$ then find f(π2)$f(\frac{\pi }{2})$. 

8. Find the area of the region enclosed by the curves y = x , x = e, y = 1x$\frac{1}{x}$ and the positive x-axis. 

9. Calculate the area of the region enclosed between the circles: x2 + y2 = 16 and (x + 4)2 + y2 = 16. 

10. Using integration, find the area of region bounded by the triangle whose vertices are (-1, 0), (1, 3) and (3, 2). 

11. Find the area of the region {(x,y);x2⩽y⩽x}$\left\{\left(x,y\right);x^2⩽y⩽x\right\}$. 

12. Evaluate limx→∞(xxx!)1/x$\underset{x\to \mathrm{\infty }}{lim}{\left(\frac{x^x}{x!}\right)}^{1/x}$. 

13. Evaluate limx→∞[1x+x2(x+1)3+x2(x+2)3+.........+18x]$\underset{x\to \mathrm{\infty }}{lim}\left[\frac{1}{x}+\frac{x^2}{(x+1{)}^3}+\frac{x^2}{(x+2{)}^3}+.........+\frac{1}{8x}\right]$. 

14. Find the area of the region enclosed by the parabola x2= y and the line y=x + 2. 

15. Using integration, find the area of the region enclosed between the two circles x2 + y2 = 4 and (x - 2)2 + y2 = 4. 

CBSE Test Paper 01
Chapter 8 Application of Integrals

---

Solution

1. (a) 3203 sq. units$\frac{320}{3}sq.units$
   Explanation: Eliminating y, we get: x4=256×20x$x^4=256\times 20x$
   ⇒x=0,x=8(10)13$\Rightarrow x=0,x=8(10{)}^{\frac{1}{3}}$
   Required area:
   =∫08(10)13(20x−−−√−x216)dx$=\underset{0}{\overset{8{(10)}^{\frac{1}{3}}}{\int }}\left(\sqrt{20x}-\frac{x^2}{16}\right)dx$
   =6403−3203=3203$=\frac{640}{3}-\frac{320}{3}=\frac{320}{3}$ sq units
2. (c) 9 sq. units
   Explanation: Given parabola is: (y−2)2=x−1⇒dydx=12(y−2)${\left(y-2\right)}^2=x-1\Rightarrow \frac{dy}{dx}=\frac{1}{2(y-2)}$
   When y= 3, x= 2
   ∴dydx=12$\therefore \frac{dy}{dx}=\frac{1}{2}$
   Therefore, tangent at ( 2, 3 ) is y – 3 = ½ ( x – 2 ). i.e. x – 2y +4 = 0 . therefore required area is: ∫03(y−2)2+1.dy−∫03(2y−4)dy$\underset{0}{\overset{3}{\int }}{(y-2)}^2+1.dy-\underset{0}{\overset{3}{\int }}(2y-4)dy$=[(y−2)33+y]30−[y2−4y]30=9$={\left[\frac{{(y-2)}^3}{3}+y\right]}_0^3-{\left[y^2-4y\right]}_0^3=9$
3. (c) 9
   Explanation: Required area: ∫09x−−√dx−∫39(x−32)dx$\underset{0}{\overset{9}{\int }}\sqrt{x}dx-\underset{3}{\overset{9}{\int }}\left(\frac{x-3}{2}\right)dx$=[x323/2]90−12[x22−3x]93=9sq.units$={\left[\frac{x^{\frac{3}{2}}}{3/2}\right]}_0^9-\frac{1}{2}{\left[\frac{x^2}{2}-3x\right]}_3^9=9sq.units$
4. (a) 23$\frac{2}{3}$
   Explanation: Required area: 2∫0a4ax−−−√dx$2\underset{0}{\overset{a}{\int }}\sqrt{4ax}dx$
   =kα(24aα−−−√)$=k\alpha (2\sqrt{4a\alpha })$
   =8a√3α32$=\frac{8\sqrt{a}}{3}{\alpha }^{\frac{3}{2}}$
   =4a−−√kα32⇒k=23$=4\sqrt{a}k{\alpha }^{\frac{3}{2}}\Rightarrow k=\frac{2}{3}$
5. (b) 2(2–√−1)$2(\sqrt{2}-1)$sq. units
   Explanation: Required area = ∫0π2|sinx−cosx|dx$\underset{0}{\overset{\frac{\pi }{2}}{\int }}\left|\sin x-\cos x\right|dx$
   =∫0π4(cosx−sinx)dx+∫π4π2(sinx−cosx)dx$=\underset{0}{\overset{\frac{\pi }{4}}{\int }}(\cos x-\sin x)dx+\underset{\frac{\pi }{4}}{\overset{\frac{\pi }{2}}{\int }}(sinx-\cos x)dx$
   =[sinx+cosx]π40+[−cosx−sinx]π2π4$={\left[\sin x+\cos x\right]}_0^{\frac{\pi }{4}}+{\left[-cosx-sinx\right]}_{\frac{\pi }{4}}^{\frac{\pi }{2}}$
   =12√+12√−(0+1)−{1−(12√+12√)}$=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-(0+1)-\left\{1-\left(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\right)\right\}$
   =42√−2=22–√−2=2(2–√−1)$=\frac{4}{\sqrt{2}}-2=2\sqrt{2}-2=2(\sqrt{2}-1)$
6. we are given,
   ∫1a[f(x)−2]dx=23[(2a)3/2−3a+3−22–√]${\int }_a^1[f(x)-2]dx=\frac{2}{3}\left[(2a{)}^{3/2}-3a+3-2\sqrt{2}\right]$
   Differentiating w.r.t a, we get
   f(a) - 2 =23[322a−−√.2−3]$=\frac{2}{3}\left[\frac{3}{2}\sqrt{2a}.2-3\right]$
   f(a)= 22a−−√,a≥1$\sqrt{2a},a\ge 1$
   ∴ f(x)=22x−−√,x≥1$\therefore f(x)=2\sqrt{2x},x\ge 1$
7. we have, ∫a0f(x)dx=a22+a2sin a+π2cos a${\int }_0^{a}f(x)dx=\frac{a^2}{2}+\frac{a}{2}sina+\frac{\pi }{2}cosa$
   Differentiating w.r.t a,we get,
   f(a)=a+ 12(sin a+acos a)−π2sin a$\frac{1}{2}(sina+acosa)-\frac{\pi }{2}sina$
   put a=π2,$\frac{\pi }{2},$ f(π2)=π2+12−π2=12$f\left(\frac{\pi }{2}\right)=\frac{\pi }{2}+\frac{1}{2}-\frac{\pi }{2}=\frac{1}{2}$
8. We have y=4x2 and y=19x2$y=4x^{2}andy=\frac{1}{9}{x}^2$
   
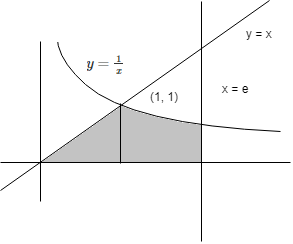
   Required area =2∫20(3y√−y√2)dy$2{\int }_0^2\left(3\sqrt{y}-\frac{\sqrt{y}}{2}\right)dy$
   =2(5y2y√3/2)20$=2{\left(\frac{5y}{2}\frac{\sqrt{y}}{3/2}\right)}_0^2$
   =2.5322–√=202√3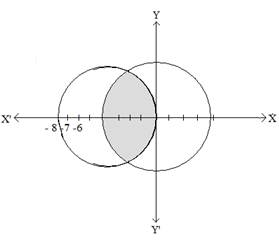$=2.\frac{5}{3}2\sqrt{2}=\frac{20\sqrt{2}}{3}$
9. 
   x2 + y2 = 16
   (x + 4)2 + y2 = 16
   Intersecting at x = -2
   Area=4∫−2−416−x2−−−−−−√dx$=4{\int }_{-4}^{-2}\sqrt{16-x^2}dx$
   =4[∫−2−442−x2−−−−−−√dx]$=4\left[{\int }_{-4}^{-2}\sqrt{4^2-x^2}dx\right]$ =4[x21−x2−−−−−√+422sin−1x4]−2−4$=4{\left[\frac{x}{2}\sqrt{1-x^2}+\frac{4^2}{2}si{n}^{-1}\frac{x}{4}\right]}_{-4}^{-2}$ =4[(−23–√−4π3)−(−4π)]$=4\left[(-2\sqrt{3}-\frac{4\pi }{3})-(-4\pi )\right]$
   =(−83–√+32π3)$=\left(-8\sqrt{3}+\frac{32\pi }{3}\right)$
10. 
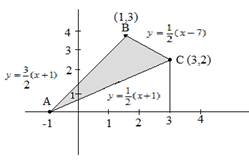
    A (-1, 0) B (1, 3) C (3, 2)
    Equation of AB
    y−y1=y2−y1x2−x1(x−x1)$y-y_1=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right)$
    y−0=3−01+1(x+1)$y-0=\frac{3-0}{1+1}\left(x+1\right)$
    y=32(x+1)$y=\frac{3}{2}\left(x+1\right)$
    Similarly,
    Equation of BC y=−12(x−7)$y=\frac{-1}{2}\left(x-7\right)$
    Equation of AC =12(x+1)$=\frac{1}{2}\left(x+1\right)$
    Area ΔABC=∫1−132(x+1)dx+∫3112(x−7)dx$\mathrm{\Delta }ABC={\int }_{-1}^1\frac{3}{2}\left(x+1\right)dx+{\int }_1^3\frac{1}{2}\left(x-7\right)dx$ −∫3−112(x+1)dx$-{\int }_{-1}^3\frac{1}{2}\left(x+1\right)dx$
    =32[x22+x]1−1+12[7x−x22]31$=\frac{3}{2}{\left[\frac{x^2}{2}+x\right]}_{-1}^1+\frac{1}{2}{\left[7x-\frac{x^2}{2}\right]}_1^3$−[x22+x]3−1$-{\left[\frac{x^2}{2}+x\right]}_{-1}^3$
    =32[(12+1)−(12−1)]+12[(21−92)−(7−12]$=\frac{3}{2}\left[(\frac{1}{2}+1)-(\frac{1}{2}-1)\right]+\frac{1}{2}\left[(21-\frac{9}{2})-(7-\frac{1}{2}\right]$
    −12[(92+3)−(12−1)]$-\frac{1}{2}\left[(\frac{9}{2}+3)-(\frac{1}{2}-1)\right]$
    =32(2)+12(10)−12(8)=3+5−4$=\frac{3}{2}(2)+\frac{1}{2}(10)-\frac{1}{2}(8)=3+5-4$
    = 4 sq. units
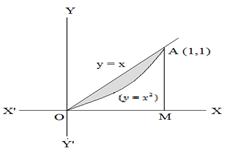
11. y = x2
    
    y = x
    ⇒$\Rightarrow$ x = 0, y = 0
    x = 1, y = 1
    Area =∫10xdx−∫10x2dx$={\int }_0^{1}xdx-{\int }_0^1{x}^{2}dx$
    =∫10(x−x2)dx$={\int }_0^1(x-x^2)dx$
    =[x22−x33]10$={\left[\frac{x^2}{2}-\frac{x^3}{3}\right]}_0^1$
    =12−13$=\frac{1}{2}-\frac{1}{3}$
    =16$=\frac{1}{6}$ sq. units
12. Given L=limx→∞(xxx!)1/x$L=\underset{x\to \mathrm{\infty }}{lim}{\left(\frac{x^x}{x!}\right)}^{1/x}$
    Taking logarithm on both sides
    log L=limx→∞1x(logx1+logx2+.....+logxx)$logL=\underset{x\to \mathrm{\infty }}{lim}\frac{1}{x}\left(log\frac{x}{1}+log\frac{x}{2}+.....+log\frac{x}{x}\right)$
    = limx→∞1x∑xr=1log xr$\underset{x\to \mathrm{\infty }}{lim}\frac{1}{x}\sum _{r=1}^{x}log\frac{x}{r}$
    =limx→∞1x∑xr=1log 1(r/x)$\underset{x\to \mathrm{\infty }}{lim}\frac{1}{x}\sum _{r=1}^{x}log\frac{1}{(r/x)}$
    =∫10log1x dx$={\int }_0^{1}log\frac{1}{x}dx$
    =−∫10log x dx$=-{\int }_0^{1}logxdx$
    =−[xlog x+x]10$=-[xlogx+x{]}_0^1$
    =−[(1log 1+1)−(0log0−0)]$=-[(1log1+1)-(0\log 0-0)]$ = 1
    ∴$\therefore$ Log L=1 $LogL=1$
    ⇒L=e$\Rightarrow L=e$
    ⇒limx→∞(xxx!)1/x=e$\Rightarrow \underset{x\to \mathrm{\infty }}{lim}{\left(\frac{x^x}{x!}\right)}^{1/x}=e$
13. Given, limx→∞[1x+x2(x+1)3+x2(x+2)3+.........+18x]$\underset{x\to \mathrm{\infty }}{lim}\left[\frac{1}{x}+\frac{x^2}{(x+1{)}^3}+\frac{x^2}{(x+2{)}^3}+.........+\frac{1}{8x}\right]$
    =limx→∞∑xr=0x2(x+r)3$=\underset{x\to \mathrm{\infty }}{lim}\sum _{r=0}^x\frac{x^2}{(x+r{)}^3}$
    =limx→∞∑xr=01/x(1+r/x)2$=\underset{x\to \mathrm{\infty }}{lim}\sum _{r=0}^x\frac{1/x}{(1+r/x{)}^2}$
    =∫10dy(1+y)3,$={\int }_0^1\frac{dy}{(1+y{)}^3},$ replace  rx$\frac{r}{x}$ by y and 1x$\frac{1}{x}$ by dy
    =[−12(1+y)2]10$={\left[\frac{-1}{2(1+y{)}^2}\right]}_0^1$
    =[−12(1+12)−−12(1+02)]$=\left[\frac{-1}{2(1+1^2)}-\frac{-1}{2(1+0^2)}\right]$
    =[−12(2)−−12(1)]$=\left[\frac{-1}{2(2)}-\frac{-1}{2(1)}\right]$
    =[−14−−12]$=\left[\frac{-1}{4}-\frac{-1}{2}\right]$ =14$=\frac{1}{4}$
14. We have, x2 = y and y = x + 2
    ⇒x2=x+2$\Rightarrow x^2=x+2$
    ⇒x2−x−2=0$\Rightarrow x^2-x-2=0$
    ⇒x2−2x+x−2=0$\Rightarrow x^2-2x+x-2=0$
    ⇒x(x−2)+1(x−2)=0$\Rightarrow x\left(x-2\right)+1\left(x-2\right)=0$
    ⇒(x+1)(x−2)=0$\Rightarrow \left(x+1\right)\left(x-2\right)=0$
    ⇒x=−1,2$\Rightarrow x=-1,2$
    
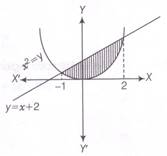
    ∴$\therefore$ Required area of shaded region, =∫2−1(x+2−x2)dx=[x22+2x−x33]2−1$={\int }_{-1}^2{\left(x+2-x^2\right)dx=\left[\frac{x^2}{2}+2x-\frac{x^3}{3}\right]}_{-1}^2$
    =(8−3−12)=92$=\left(8-3-\frac{1}{2}\right)=\frac{9}{2}$
15. Given circles are x2+y2=4$x^2+y^2=4$...(i)
    (x−2)2+y2=4$(x-2{)}^2+y^2=4$...(ii)
    Eq. (i) is a circle with centre origin and
    Radius = 2.
    Eq. (ii) is a circle with centre C (2, 0) and
    Radius = 2.
    On solving Eqs. (i) and (ii), we get
    (x−2)2+y2=x2+y2$(x-2{)}^2+y^2=x^2+y^2$
    ⇒x2 - 4x+4+y2=x2+y2$\Rightarrow x^2\text{ - }4x+4+y^2=x^2+y^2$
    ⇒x=1$\Rightarrow x=1$
    On putting x = 1 in Eq. (i), we get
    y=±3–√$y=\pm \sqrt{3}$
    Thus, the points of intersection of the given circles are A (1, 3–√$\sqrt{3}$) and A'(1,-3–√$\sqrt{3}$).
    
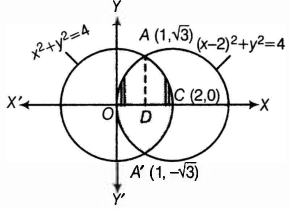
    Clearly, required area= Area of the enclosed region OACA'O between circles
    = 2 [ Area of the region ODCAO]
    =2 [Area of the region ODAO + Area of the region DCAD]
    =2[∫10y2dx+∫21y1dx]$=2\left[{\int }_0^1{y}_{2}dx+{\int }_1^2{y}_{1}dx\right]$
    =2[∫104−(x−2)2−−−−−−−−−−√dx+∫214−x2−−−−−√dx]$=2\left[{\int }_0^1\sqrt{4-(x-2{)}^2}dx+{\int }_1^2\sqrt{4-x^2}dx\right]$
    =2[12(x−2)4−(x−2)2−−−−−−−−−−√+12×4sin−1(x−22)]10$=2{\left[\frac{1}{2}(x-2)\sqrt{4-(x-2{)}^2}+\frac{1}{2}\times 4{\sin }^{-1}\left(\frac{x-2}{2}\right)\right]}_0^1$+2[12x4−x2−−−−−√+12×4sin−1x2]21$+2{\left[\frac{1}{2}x\sqrt{4-x^2}+\frac{1}{2}\times 4{\sin }^{-1}\frac{x}{2}\right]}_1^2$
    =[(x−2)4−(x−2)2−−−−−−−−−−√+4sin−1(x−22)]10$={\left[(x-2)\sqrt{4-(x-2{)}^2}+4{\sin }^{-1}\left(\frac{x-2}{2}\right)\right]}_0^1$+[x4−x2−−−−−√+4sin−1x2]21$+{\left[x\sqrt{4-x^2}+4{\sin }^{-1}\frac{x}{2}\right]}_1^2$
    =[{−3–√+4sin−1(−12)}−0−4sin−1(−1)]$=\left[\left\{-\sqrt{3}+4{\sin }^{-1}\left(\frac{-1}{2}\right)\right\}-0-4{\sin }^{-1}(-1)\right]$+[0+4sin−11−3–√−4sin−112]$+\left[0+4{\sin }^{-1}1-\sqrt{3}-4{\sin }^{-1}\frac{1}{2}\right]$
    =[(−3–√−4×π6)+4×π2]+$=\left[\left(-\sqrt{3}-4\times \frac{\pi }{6}\right)+4\times \frac{\pi }{2}\right]+$[4×π2−3–√−4×π6]$\left[4\times \frac{\pi }{2}-\sqrt{3}-4\times \frac{\pi }{6}\right]$
    =(−3–√−2π3+2π)+(2π−3–√−2π3)$=\left(-\sqrt{3}-\frac{2\pi }{3}+2\pi \right)+\left(2\pi -\sqrt{3}-\frac{2\pi }{3}\right)$
    =8π3−23–√$=\frac{8\pi }{3}-2\sqrt{3}$ sq units.