Differential Equations - Revision Notes

CBSE Class 12 Mathematics

Chapter-9 Differential Equations

Differential Equation: An equation involving derivatives of the dependent variable with respect to independent variable (variables) is known as a differential equation.
Linear and non-linear differential equation: A differential equation is said to be linear if unknown function (dependent variable) as its derivative which occurs in the equation, occur only in the first degree and are not multiplied together. Otherwise the differential equaiton is said to be non-linear.
Order: Order of a differential equation is the order of the highest order derivative occurring in the differential equation.
Degree: Degree of a differential equation is defined if it is a polynomial equation in its derivatives.
Degree (when defined) of a differential equation is the highest power (positive integer only) of the highest order derivative in it.
Solution: A function which satisfies the given differential equation is called its solution.
General Solution: The solution which contains as many arbitrary constants as the order of the differential equation is called a general solution.
Particular Solution: The solution free from arbitrary constants is called particular solution.
To form a differential equation from a given function we differentiate the function successively as many times as the number of arbitrary constants in the given function and then eliminate the arbitrary constants.
Variable Separable method: Variable separable method is used to solve such an equation in which variables can be separated completely i.e. terms containing y should remain with dy and terms containing x should remain with dx.
A differential equation which can be expressed in the form 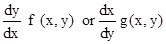where, f(x , y) and g (x , y) are homogenous functions of degree zero is called a homogeneous differential equation.
A differential equation of the form 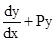= Q, where P and Q are constants or functions of x only is called a first order linear differential equation.