Continuity and Differentiability - Exemplar Solutions
CBSE Class–12 Mathematics
NCERT Exemplar
Chapter - 5
CONTINUITY AND DIFFERENTIABILITY - Short Answer Questions
1. Find the value of the constant k so that the function  defined below is continuous at
defined below is continuous at 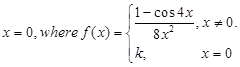
Sol. It is given that the function  is continuous at x = 0. Therefore,
is continuous at x = 0. Therefore, 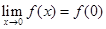





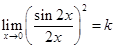

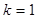
Thus,  is continuous at x = 0 if k = 1.
is continuous at x = 0 if k = 1.
2. Discuss the continuity of the function  .
.
Sol. Since sin x and cos x are continuous functions and product of two continuous
function is a continuous function, therefore  is a continuous function.
is a continuous function.
3. If 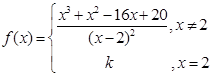 is continuous at x = 2, find the value of k.
is continuous at x = 2, find the value of k.
Sol. Given  = k.
= k.
Now, 
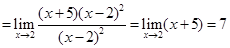
As  is continuous at x= 2, we have
is continuous at x= 2, we have

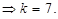
4. Show that the function  defined by
defined by
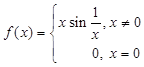 is continuous at x = 0.
is continuous at x = 0.
Sol. Left hand limit at x = 0 is given by
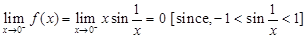
Similarly, 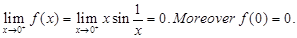
Thus, 
5. Given 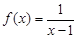 . Find the points of discontinuity of the composite function
. Find the points of discontinuity of the composite function 
Sol. We know that 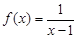 is discontinuous at x = 1
is discontinuous at x = 1
Now, for x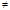 1,
1,
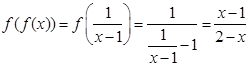
Which is discontinuous at x = 2.
Hence, the points of discontinuity are x = 1 and x = 2.
6. Let 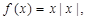 for all
for all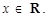 Discuss the derivability of
Discuss the derivability of 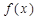 at x = 0
at x = 0
Sol. We may rewrite  as
as 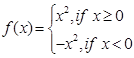
Now, 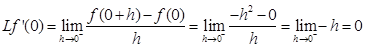
Now, 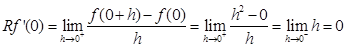
Since the left-hand derivative and right hand derivative both are equal, hence  is differentiable at x = 0.
is differentiable at x = 0.
7. Differentiate 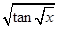 w.r.t. x
w.r.t. x
Sol. Let  . Using chain rule, we get
. Using chain rule, we get
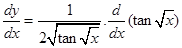
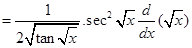
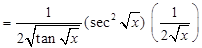
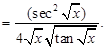
8. If 
Sol. Given y = tan (x + y). differentiating both sides w.r.t. x, we get
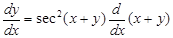
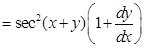

Therefore, 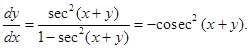
9. If 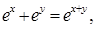 prove that
prove that 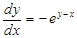
Sol. Given that  Differentiating both sides w.r.t. x, we have
Differentiating both sides w.r.t. x, we have

Which implies that 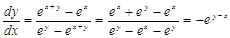
10. Find 
Sol. Put x = tan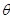 , where
, where 
Therefore, 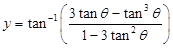
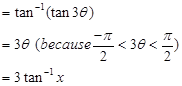
Hence, 
11. If 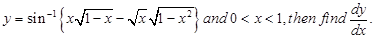
Sol. We have 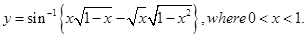
Put 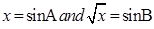
Therefore, 
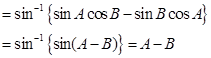
Thus 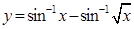
Differentiating w.r.t. x, we get

12. If 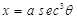 and
and 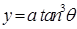 , find
, find 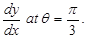
Sol. We have x = a sec3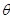 and y = a tan3
and y = a tan3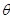 .
.
Differentiating w.r.t.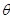 , we get
, we get
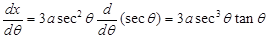
and 
Thus 
Hence 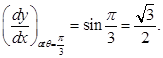
13. If 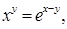 prove that
prove that 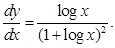
Sol. We have 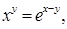 Taking logarithm on both sides, we get
Taking logarithm on both sides, we get
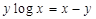


i.e. 
Differentiating both sides w.r.t. x, we get

14. If  , prove that
, prove that 
Sol. We have  . Differentiating w.r.t. x, we get
. Differentiating w.r.t. x, we get

Thus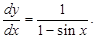
Now, differentiating again w.r.t. x, we get
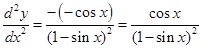
15. If 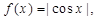 find
find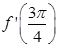 .
.
Sol. When  < x <
< x <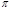 , cos x < 0 so that
, cos x < 0 so that  = - cos x, i.e., f (x) = - cos x
= - cos x, i.e., f (x) = - cos x  f ‘ (x) = sin x.
f ‘ (x) = sin x.
Hence, 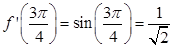
16. If 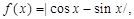 find
find 
Sol. When 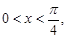 cos x >sin x, so that cos x – sin x > 0, i.e.,
cos x >sin x, so that cos x – sin x > 0, i.e.,


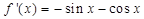
Hence, 
17. Verify Rolle’s theorem for the function, 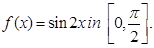
Sol. Given 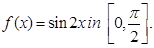 Note that:
Note that:
(i) The function  is continuous in
is continuous in 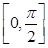 as
as  is a sine function, which is always continuous.
is a sine function, which is always continuous.
(ii)  exists in
exists in 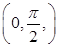 , hence
, hence  is derivable in
is derivable in 
(iii) 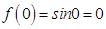 and
and 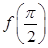 = sin
= sin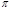 = 0
= 0 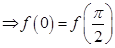 .
.
Conditions of Rolle’s theorem are satisfied. Hence there exists at least one 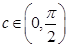 such that
such that 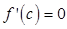 . Thus
. Thus

18. Verify mean value theorem for the function 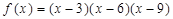 in [3, 5].
in [3, 5].
Sol. (i) Function  is continuous in [3, 5] as product of polynomial functions is a polynomial, which is continuous.
is continuous in [3, 5] as product of polynomial functions is a polynomial, which is continuous.
(ii) 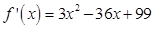 exists in (3, 5) and hence derivable in (3, 5).
exists in (3, 5) and hence derivable in (3, 5).
Thus conditions of mean value theorem are satisfied. Hence, there exists at least one 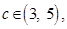 such that
such that
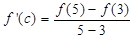




Hence 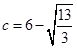 (since other value is not permissible).
(since other value is not permissible).
19. If  find the value of
find the value of 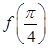 so that
so that 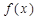 becomes continuous at
becomes continuous at 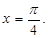
Sol. Given, 
Therefore, 
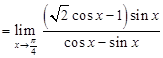
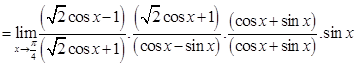
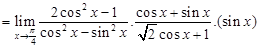

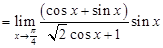
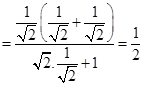
Thus, 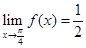
If we define 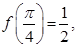 then
then 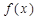 will become continuous at
will become continuous at 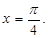 Hence for
Hence for  to be continuous at
to be continuous at 
20. Show that the function  given by
given by 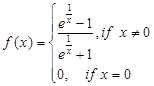 is discontinuous at x = 0.
is discontinuous at x = 0.
Sol. The left hand limit of  at x = 0 is given by
at x = 0 is given by
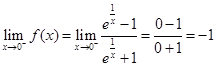
Similarly, 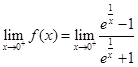
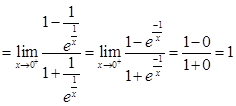
Thus 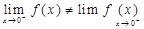 therefore,
therefore, 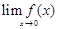 does not exist. Hence
does not exist. Hence  is discontinuous at x = 0.
is discontinuous at x = 0.
21. Let 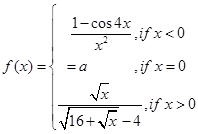
For what value of a,  is continuous at x = 0?
is continuous at x = 0?
Sol. Here 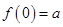 Left-hand limit of
Left-hand limit of  at 0 is
at 0 is

and right hand limit of  at 0 is
at 0 is
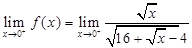
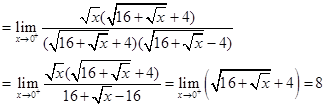
Thus, 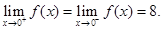 Hence
Hence  is continuous at x = 0 only if a = 8.
is continuous at x = 0 only if a = 8.
22. Examine the differentiability of the function  defined by
defined by

Sol. The only doubtful points for differentiability of 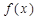 are x = –2 and x = 0. Differentiability at x = - 2.
are x = –2 and x = 0. Differentiability at x = - 2.
Now 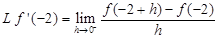

and 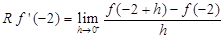
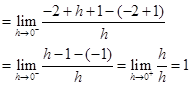
Thus  Therefore
Therefore  is not differentiable at x = -2.
is not differentiable at x = -2.
Similarly, for differentiability at x = 0, we have

which does not exist. Hence  is not differentiable at x = 0.
is not differentiable at x = 0.
23. Differentiate  with respect to
with respect to 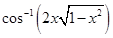 , where
, where 
Sol. Let  and
and 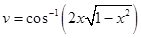 .
.
We want to find 
Now 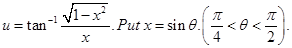
Then 

Hence 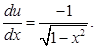
Now 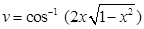
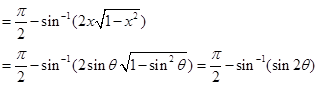
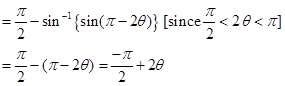



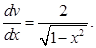
Hence 
Choose the correct answer from the given four options in each of the Examples 24 to 35.
24. The function 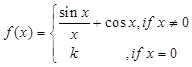 is continuous at x = 0, then the value of k is
is continuous at x = 0, then the value of k is
(A) 3
(B) 2
(C) 1
(D) 1.5
Sol. (B) is the Correct answer.
25. The function 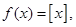 where [x] denotes the greatest integer function, is continuous at
where [x] denotes the greatest integer function, is continuous at
(A) 4
(B) - 2
(C) 1
(D) 1.5
Sol. (D) is the correct answer. The greatest integer function[x] is discontinuous at all integral values of x. Thus D is the correct answer.
26. The number of points at which the function  is not continuous is
is not continuous is
(A) 1
(B) 2
(C) 3
(D) None of these
Sol. (D) is the correct answer. As x – [x] = 0, when x is an integer so 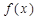 is discontinuous for all
is discontinuous for all 
27. The function given by 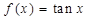 is discontinuous on the set
is discontinuous on the set
(A) 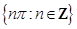
(B) 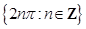
(C) 
(D) 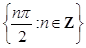
Sol. C is the correct answer.
28. Let 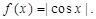 Then
Then
(A)  is everywhere differentiable.
is everywhere differentiable.
(B)  is everywhere continuous but not differentiable at
is everywhere continuous but not differentiable at 
(C)  is everywhere continuous but not differentiable at
is everywhere continuous but not differentiable at 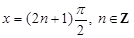
(D) None of these.
Sol. C is the correct answer.
29. The function  is
is
(A) continuous at x = 0 as well as at x = 1.
(B) continuous at x = 1 but not at x = 0.
(C) discontinuous at x = 0 as well as at x = 1.
(D) continuous at x = 0 but not at x = 1.
Sol. Correct answer is A.
30. The value of k which makes the function defined by
(A) 8
(B) 1
(C) -1
(D) None of these
Sol. (D) is the correct answer. Indeed  does not exist.
does not exist.
31. The set of points where the functions f given by 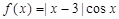 differentiable is
differentiable is
(A) R
(B) 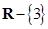
(C) 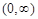
(D) None of these
Sol. B is the correct answer.
32. Differential coefficient of sec (tan-1 x) w.r.t. x is
(A) 
(B) 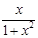
(C) 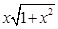
(D) 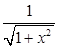
Sol. (A) is the correct answer.
33. If  and
and  then
then  is
is
(A) 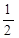
(B) x
(C) 
(D) 1
Sol. (D) is the correct answer.
34. The value of c in Rolle’s Theorem for the function 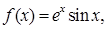
 is
is
(A) 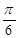
(B) 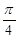
(C) 
(D) 
Sol. (D) is the correct answer.
35. The value of c in Mean value theorem for the function 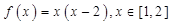 is
is
(A) 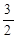
(B) 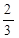
(C) 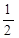
(D) 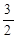
Sol. (A) is the correct answer.
36. Match the following
COLUMN – I | COLUMN – II |
(A) If a function | (A) |x| |
(B) Every continuous function is differentiable | (B) True |
(C) An example of a function which is continuous everywhere but not differentiable at exactly one point | (C) 6 |
(D) The identify function i.e. | (D) False |
Sol. 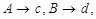

Fill in the blanks in each of the Examples 37 to 41.
37. The number of points at which the function  is discontinuous is _____________.
is discontinuous is _____________.
Sol. The given function is discontinuous at x = 0, 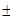 1 and hence the number of points of discontinuity is 3.
1 and hence the number of points of discontinuity is 3.
38. If 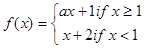 is continuous, then a should be equal to ____________.
is continuous, then a should be equal to ____________.
Sol. a = 2
39. The derivative of  w.r.t. x is _____________.
w.r.t. x is _____________.
Sol. 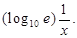
40. If 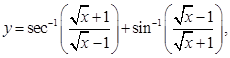 then
then  is equal to ___________.
is equal to ___________.
Sol. 0.
41. The derivative of sin x w.r.t. cos x is ___________.
Sol. –cot x
Sate whether the statements are True of False in each of the Exercises 42 to 46.
42. For continuity, at x = a, each of  and
and 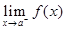 is equal to
is equal to 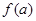 .
.
Sol. True.
43. y = |x – 1| is a continuous function.
Sol. True.
44. A continuous function can have some points where limit does not exist.
Sol. False.
45. |sin x| is a differentiable function for every value of x.
Sol. False.
46. cos |x| is differentiable everywhere.
Sol. True.
 is continuous at x = 0, then k is equal to
is continuous at x = 0, then k is equal to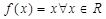 is a continuous function.
is a continuous function.