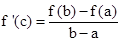Continuity and Differentiability - Revision Notes

 CBSE Class 12 Mathematics

Chapter-5
Continuity and Differentiability

---

• Continuity of function at a point: Geometrically we say that a funciton y=f(x)$y=f\left(x\right)$ is continuous at x=a$x=a$ if the graph of the function y=f(x)$y=f\left(x\right)$ is continuous (without any break) at x=a$x=a$.
• A funciton f(x)$f\left(x\right)$ is said to be continuous at a point x=a$x=a$ if:

         (i)     f(a)$f\left(a\right)$ exists i.e., f(a)$f\left(a\right)$ is finite, definite and real.

         (ii)    limx→af(x)$\underset{x\to a}{lim}f\left(x\right)$ exists.

         (iii)   limx→af(x)=f(a)$\underset{x\to a}{lim}f\left(x\right)=f\left(a\right)$

• A function f(x)$f\left(x\right)$ is continuous at x=a$x=a$  if limh→0f(a+h)=limh→0f(a+h)=f(a)$\underset{h\to 0}{lim}f\left(a+h\right)=\underset{h\to 0}{lim}f\left(a+h\right)=f\left(a\right)$ where h→0$h\to 0$ through positive values.
• Continuity of a function in a closed interval: A function f(x)$f\left(x\right)$ is said to be continuous in the closed interval  if it is continuous for every value of x$x$ lying between a and b continuous to the right of a and to the left of x=b$x=b$ i.e., limx→a−0f(x)=f(a)$\underset{x\to a-0}{lim}f\left(x\right)=f\left(a\right)$ and limx→b−0f(x)=f(b)$\underset{x\to b-0}{lim}f\left(x\right)=f\left(b\right)$
• Continuity of a function in a open interval: A function f(x)$f\left(x\right)$ is said to be continuous in an open interval (a,b)$\left(a,b\right)$ if it is continuous at every point in  (a,b)$\left(a,b\right)$.
• Discontinuity (Discontinuous function): A function f(x)$f\left(x\right)$ is said to be discontinuous in an interval if it is discontinuous even at a single point of the interval.
• Suppose f$f$ is a real function and c$c$ is a point in its domain. The derivative of f$f$ at c$c$ is defined by f′(c)=limh→0f(c+h)−f(c)h$f^{\prime }\left(c\right)=\underset{h\to 0}{lim}\frac{f\left(c+h\right)-f\left(c\right)}{h}$ provided this limit exists.
• A real valued function is continuous at a point in its domain if the limit of the function at that point equals the value of the function at that point. A function is continuous if it is continuous on the whole of its domain.
• dydx$\frac{dy}{dx}$ is derivative of first order and is also denoted by y′$y^{\prime }$ or y1$y_1$.
• Sum, difference, product and quotient of continuous functions are continuous. i.e., if f and g are continuous functions, then 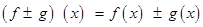 is continuous. (f . g) (x) = f (x) . g(x) is continuous.

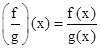         (wherever g (x) ≠ 0) is continuous.

• Every differentiable function is continuous, but the converse is not true.
• Chain rule is rule to differentiate composites of functions. If f = v o u, t = u (x) and if both 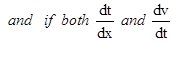exist then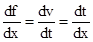
• Following are some of the standard derivatives (in appropriate domains):
• (u±v)′=u′±v′${\left(u\pm v\right)}^{\prime }=u^{\prime }\pm v^{\prime }$
• (uv)′=u′v+uv′${\left(uv\right)}^{\prime }=u^{\prime }v+u{v}^{\prime }$ [Product Rule]
• (uv)′=u′v−uv′v2${\left(\frac{u}{v}\right)}^{\prime }=\frac{u^{\prime }v-u{v}^{\prime }}{v^2}$, wherever v≠0$v\ne 0$ [Quotient Rule]
• If y=f(u);u=g(x),$y=f\left(u\right);u=g\left(x\right),$ then dydx=dydu×dudx$\frac{dy}{dx}=\frac{dy}{du}\times \frac{du}{dx}$ [Chain Rule]
• If x=f(t);y=g(t)$x=f\left(t\right);y=g\left(t\right)$, then dydx=dydt÷dxdt$\frac{dy}{dx}=\frac{dy}{dt}÷\frac{dx}{dt}$ [Parametric Form]
• ddx(xn)=nxn−1$\frac{d}{dx}\left(x^n\right)=n{x}^{n-1}$
• ddx(sinx)=cosx$\frac{d}{dx}\left(\sin x\right)=\cos x$
• ddx(cosx)=−sinx$\frac{d}{dx}\left(\cos x\right)=-\sin x$
• ddx(tanx)=−sec2x$\frac{d}{dx}\left(\tan x\right)=-{\sec }^{2}x$
• ddx(cotx)=−cosec2x$\frac{d}{dx}\left(\cot x\right)=-\cos e{c}^{2}x$
• ddx(secx)=secx.tanx$\frac{d}{dx}\left(\sec x\right)=\sec x.\tan x$
• ddx(cosecx)=−cosecx.cotx.$\frac{d}{dx}\left(\cos ecx\right)=-\cos ecx.\cot x.$
• ddx(ax)=ax.logea$\frac{d}{dx}\left(a^x\right)=a^x.{\log }_{e}a$
• ddx(logex)=1x$\frac{d}{dx}\left({\log }_{e}x\right)=\frac{1}{x}$
•     
• 
•                    
• ddx(cos−1x)=−11+x2$\frac{d}{dx}\left({\cos }^{-1}x\right)=\frac{-1}{1+x^2}$
•   
• 
•                                 
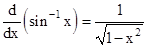
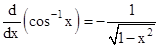
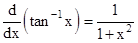
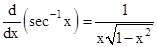
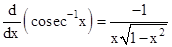
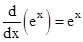
• Logarithmic differentiation is a powerful technique to differentiate functions of the form 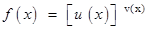   Here both f (x) and u (x) need to be positive for this technique to make sense.
• If we have to differentiate logarithmic funcitons, other than base e$e$, then we use the result logba=logealogeb${\log }_{b}a=\frac{{\log }_{e}a}{{\log }_{e}b}$ and then differentiate R.H.S.
• While differentiating inverse trigonometric functions, first represent it in simplest form by using suitable substitution and then differentiate simplified form.
• If we are given implicit functions then differentiate directly w.r.t. suitable variable involved and get the derivative by readusting the terms.
• d2ydx2=ddx(dydx)$\frac{d^{2}y}{d{x}^2}=\frac{d}{dx}\left(\frac{dy}{dx}\right)$ is derivative of second order and is denoted by y′′$y^{″}$ or y2$y_2$.
• Rolle’s Theorem: If f: [a, b] → R is continuous on [a, b] and differentiable on (a, b) such that f (a) = f (b), then there exists some c in (a, b) such that f ′(c) = 0.
• Lagrange's Mean Value Theorem: If f: [a, b] → R is continuous on [a, b] and differentiable on (a, b). Then there exists some c in (a, b) such that