Determinants - Test Papers

 CBSE Test Paper 01

Chapter 4 Determinants

---

1. The roots of the equation det. ∣∣∣∣1−x0022−x2303−x∣∣∣∣=0$\left|\begin{array}{ccc}1-x& 2& 3\\ 0& 2-x& 0\\ 0& 2& 3-x\end{array}\right|=0$ are 
   1. None of these
   2. 2 and 3
   3. 1, 2 and 3
   4. 1 and 3
2. If A’ is the transpose of a square matrix A, then 
   1. |A| + |A'| = 0
   2. |A| = |A'|
   3. |A| ≠$\ne$ |A'|
   4. None of these
3. If f(x) = ∣∣∣∣2cosx1012cosx1012cosx∣∣∣∣$\left|\begin{array}{ccc}2\cos x& 1& 0\\ 1& 2\cos x& 1\\ 0& 1& 2\cos x\end{array}\right|$ then, f (π3$\frac{\pi }{3}$) =. 
   1. 0
   2. 1
   3. -1
   4. 2
4. The roots of the equation ∣∣∣∣1114−22x2055x2∣∣∣∣=0$\left|\begin{array}{ccc}1& 4& 20\\ 1& -2& 5\\ 1& 2x& 5x^2\end{array}\right|=0$ are 
   1. –1, –2
   2. –1, 2
   3. 1, –2
   4. 1, 2
5. If A and B are any 2 × 2$\text{2 }\times \text{ 2}$ matrices , then det. (A+B) = 0 implies 
   1. det A + det B = 0
   2. det A = 0 or det B = 0
   3. None of these
   4. det A = 0 and det B = 0
6. If ∣∣∣2x85x∣∣∣=∣∣∣6853∣∣∣$\left|\begin{array}{cc}2x& 5\\ 8& x\end{array}\right|=\left|\begin{array}{cc}6& 5\\ 8& 3\end{array}\right|$, then x is ________.
7. Multiplying a determinant by k means multiplying the elements of only one row (or one column) by ________.
8. If elements of a row (or a column) in a determinant can be expressed as the sum of two or more elements, then the given determinant can be expressed as the ________ of two or more determinants.
9. Find adj A for A=[2134].$A=\left[\begin{array}{cc}2& 3\\ 1& 4\end{array}\right].$ 
10. A=[1428]$A=\left[\begin{array}{cc}1& 2\\ 4& 8\end{array}\right]$is singular or not. 
11. Evaluate 2∣∣∣7−10−25∣∣∣$2\left|\begin{array}{rr}7& -2\\ -10& 5\end{array}\right|$. 
12. Evaluate: ∣∣∣∣cosαcosβ−sinβsinαcosβcosαsinβcosβsinαsinβ−sinα0cosα∣∣∣∣$\left|\begin{array}{ccc}\cos \alpha \cos \beta & \cos \alpha \sin \beta & -\sin \alpha \\ -\sin \beta & \cos \beta & 0\\ \sin \alpha \cos \beta & \sin \alpha \sin \beta & \cos \alpha \end{array}\right|$. 
13. Find the area of Δ$\mathrm{\Delta }$whose vertices are (3, 8) (-4, 2) and (5, 1). 
14. Find the equation of the line joining A (1, 3) and B (0, 0) using det. Find K if D (K, 0) is a point such that area of ΔABD$\mathrm{\Delta }ABD$ is 3 square unit. 
15. If A = ⎡⎣⎢10−2−2−12341⎤⎦⎥$\left[\begin{array}{ccc}1& -2& 3\\ 0& -1& 4\\ -2& 2& 1\end{array}\right]$, then find (A')-1. 
16. If A=[3−1−42],$A=\left[\begin{array}{cc}3& -4\\ -1& 2\end{array}\right],$ find matrix B such that AB = I. 
17. Using properties of determinants, prove that
    ∣∣∣∣b+cq+ry+zc+ar+pz+xa+bp+qx+y∣∣∣∣=2∣∣∣∣apxbqycrz∣∣∣∣$\left|\begin{array}{ccc}b+c& c+a& a+b\\ q+r& r+p& p+q\\ y+z& z+x& x+y\end{array}\right|=2\left|\begin{array}{ccc}a& b& c\\ p& q& r\\ x& y& z\end{array}\right|$.
18. Given A=⎡⎣⎢112−1−211−23⎤⎦⎥$A=\left[\begin{array}{ccc}1& -1& 1\\ 1& -2& -2\\ 2& 1& 3\end{array}\right]$ and B=⎡⎣⎢−4−7541−343−1⎤⎦⎥$B=\left[\begin{array}{ccc}-4& 4& 4\\ -7& 1& 3\\ 5& -3& -1\end{array}\right]$. find AB and use this result in solving the following system of equation.
    x - y + z = 4, x - 2y - 2z = 9, 2x + y + 3z = 1

CBSE Test Paper 01
Chapter 4 Determinants

---

Solution

1. 3. 1 , 2 and 3
      Explanation: Expanding along C1
      ∣∣∣∣1−x0022−x2303−x∣∣∣∣=0⇒$\left|\begin{array}{ccc}1-x& 2& 3\\ 0& 2-x& 0\\ 0& 2& 3-x\end{array}\right|=0\Rightarrow$ (1 - x)(2 - x)(3 - x) = 0⇒$\Rightarrow$ x = 1, 2 ,3.
2. 2. |A| = |A'|
      Explanation: The determinant of a matrix A and its transpose always same. Because if we interchange the rows into column in a determinant the value of determinant remains unaltered.
3. 3. –1
      Explanation: ∣∣∣∣2cosx1012cosx1012cosx∣∣∣∣$\left|\begin{array}{ccc}2\cos x& 1& 0\\ 1& 2\cos x& 1\\ 0& 1& 2\cos x\end{array}\right|$
      Put x = π3$\frac{\pi }{3}$, ∣∣∣∣∣2cosπ31012cosπ31012cosπ3∣∣∣∣∣$\left|\begin{array}{ccc}2\cos \frac{\pi }{3}& 1& 0\\ 1& 2\cos \frac{\pi }{3}& 1\\ 0& 1& 2\cos \frac{\pi }{3}\end{array}\right|$
      ⇒∣∣∣∣∣2.121012.121012.12∣∣∣∣∣$\Rightarrow \left|\begin{array}{ccc}2.\frac{1}{2}& 1& 0\\ 1& 2.\frac{1}{2}& 1\\ 0& 1& 2.\frac{1}{2}\end{array}\right|$
      ⇒∣∣∣∣110111011∣∣∣∣$\Rightarrow \left|\begin{array}{ccc}1& 1& 0\\ 1& 1& 1\\ 0& 1& 1\end{array}\right|$⇒1(0)−1(1)=−1$\Rightarrow 1(0)-1(1)=-1$
4. 2. –1 , 2
      Explanation: ∣∣∣∣1114−22x2055x2∣∣∣∣=0$\left|\begin{array}{ccc}1& 4& 20\\ 1& -2& 5\\ 1& 2x& 5x^2\end{array}\right|=0$
      Apply, R3→$\to$R3 - R1, R2→$\to$R2 - R1,
      ⇒$\Rightarrow$ ∣∣∣∣1004−62x−420−155x2−20∣∣∣∣=0$\left|\begin{array}{ccc}1& 4& 20\\ 0& -6& -15\\ 0& 2x-4& 5x^2-20\end{array}\right|=0$
      ⇒$\Rightarrow$ -6(5x2 - 20) + 15(2x - 4) =0
      ⇒$\Rightarrow$ (x - 2)(x + 1) = 0 ⇒$\Rightarrow$ x= 2 , -1.
5. 3. None of these
      Explanation: If det (A+B)=0 implies that A+B a Singular matrix.
6. x = ±$\pm$3
7. k
8. sum
9. adjA=[4−1−32]$adjA=\left[\begin{array}{cc}4& -3\\ -1& 2\end{array}\right]$
   
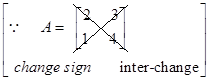
10. |A|=∣∣∣1428∣∣∣$\left|A\right|=\left|\begin{array}{cc}1& 2\\ 4& 8\end{array}\right|$
    = 8 - 8
    = 0
    Hence A is singular
11. According to the question, we have to evaluate 2∣∣∣7−10−25∣∣∣$2\left|\begin{array}{rr}7& -2\\ -10& 5\end{array}\right|$.
    Now, 2∣∣∣7−10−25∣∣∣=2[35−(20)]$2\left|\begin{array}{rr}7& -2\\ -10& 5\end{array}\right|=2[35-(20)]$
    =2×15=30$=2\times 15=30$
12. Let Δ=∣∣∣∣cosαcosβ−sinβsinαcosβcosαsinβcosβsinαsinβ−sinα0cosα∣∣∣∣$\mathrm{\Delta }=\left|\begin{array}{ccc}\cos \alpha \cos \beta & \cos \alpha \sin \beta & -\sin \alpha \\ -\sin \beta & \cos \beta & 0\\ \sin \alpha \cos \beta & \sin \alpha \sin \beta & \cos \alpha \end{array}\right|$
    Expanding along first row,
    =cosαcosβ(cosαcosβ−0)$=\cos \alpha \cos \beta \left(\cos \alpha \cos \beta -0\right)$ −cosαsinβ(−cosαsinβ−0)$-\cos \alpha \sin \beta \left(-\cos \alpha \sin \beta -0\right)$ −sinα(−sinαsin2β−sinαcos2β)$-\sin \alpha \left(-\sin \alpha {\sin }^2\beta -\sin \alpha {\cos }^2\beta \right)$
    =cos2αcos2β+cos2αsin2β$={\cos }^2\alpha {\cos }^2\beta +{\cos }^2\alpha {\sin }^2\beta$ +sin2α(sin2β+cos2β)$+{\sin }^2\alpha \left({\sin }^2\beta +{\cos }^2\beta \right)$
    =cos2α(cos2β+sin2β)$={\cos }^2\alpha \left({\cos }^2\beta +{\sin }^2\beta \right)$ +sin2α(sin2β+cos2β)$+{\sin }^2\alpha \left({\sin }^2\beta +{\cos }^2\beta \right)$
    =cos2α+sin2α$={\cos }^2\alpha +{\sin }^2\alpha$
    = 1
13. Δ=12∣∣∣∣x1x2x3y1y2y3111∣∣∣∣$\mathrm{\Delta }=\frac{1}{2}\left|\begin{array}{ccc}{x}_1& y_1& 1\\ x_2& y_2& 1\\ x_3& y_3& 1\end{array}\right|$
    =12∣∣∣∣3−45821111∣∣∣∣$=\frac{1}{2}\left|\begin{array}{ccc}3& 8& 1\\ -4& 2& 1\\ 5& 1& 1\end{array}\right|$
    =12[3(2−1)−8(−4−5)+1(−4+10)]$=\frac{1}{2}\left[3\left(2-1\right)-8\left(-4-5\right)+1\left(-4+10\right)\right]$
    =12[3+72−14]=612$=\frac{1}{2}\left[3+72-14\right]=\frac{61}{2}$
14. Let P (x, y) be any point on AB. Then the equation of line AB is,
    12∣∣∣∣01x03y111∣∣∣∣=0$\frac{1}{2}\left|\begin{array}{ccc}0& 0& 1\\ 1& 3& 1\\ x& y& 1\end{array}\right|=0$
    y = 3x
    Area ΔABD=3$\mathrm{\Delta }ABD=3$ square unit
    12∣∣∣∣10K300111∣∣∣∣=±3$\frac{1}{2}\left|\begin{array}{ccc}1& 3& 1\\ 0& 0& 1\\ K& 0& 1\end{array}\right|=\pm 3$
    k=±2$k=\pm 2$
15. If A = ⎡⎣⎢10−2−2−12341⎤⎦⎥$\left[\begin{array}{ccc}1& -2& 3\\ 0& -1& 4\\ -2& 2& 1\end{array}\right]$, then we have to find (A')-1.
    Now, A = ⎡⎣⎢10−2−2−12341⎤⎦⎥$\left[\begin{array}{ccc}1& -2& 3\\ 0& -1& 4\\ -2& 2& 1\end{array}\right]$ Therefore, we have, |A|=∣∣∣∣10−2−2−12341∣∣∣∣$|A|=\left|\begin{array}{ccc}1& -2& 3\\ 0& -1& 4\\ -2& 2& 1\end{array}\right|$
    = 1 (-1 - 8) + 2 (0 + 8) + 3 (0 - 2)
    [expanding along R1]
    =-9+16-6=1≠$\ne$0
    Therefore, A is non-singular matrix and hence its inverse exists.
    Cofactors of an element of |A| are given by
    A11=(−1)1+1∣∣∣−1241∣∣∣=(−1−8)=−9$A_{11}=(-1{)}^{1+1}\left|\begin{array}{cc}-1& 4\\ 2& 1\end{array}\right|=(-1-8)=-9$
    A12=(−1)1+2∣∣∣0−241∣∣∣=−(0+8)=−8$A_{12}=(-1{)}^1+2\left|\begin{array}{cc}0& 4\\ -2& 1\end{array}\right|=-(0+8)=-8$
    A13=(−1)1+3∣∣∣0−2−12∣∣∣=(0−2)=−2$A_{13}=(-1{)}^{1+3}\left|\begin{array}{cc}0& -1\\ -2& 2\end{array}\right|=(0-2)=-2$
    A21=(−1)2+1∣∣∣−2231∣∣∣=−(−2−6)=8$A_{21}=(-1{)}^{2+1}\left|\begin{array}{cc}-2& 3\\ 2& 1\end{array}\right|=-(-2-6)=8$
    A22=(−1)2+2∣∣∣1−231∣∣∣=(1+6)=7$A_{22}=(-1{)}^{2+2}\left|\begin{array}{cc}1& 3\\ -2& 1\end{array}\right|=(1+6)=7$
    A23=(−1)2+3∣∣∣1−2−22∣∣∣=−(2−4)=2$A_{23}=(-1{)}^{2+3}\left|\begin{array}{cc}1& -2\\ -2& 2\end{array}\right|=-(2-4)=2$
    A31=(−1)3+1∣∣∣−2−134∣∣∣=(−8+3)=−5$A_{31}=(-1{)}^{3+1}\left|\begin{array}{cc}-2& 3\\ -1& 4\end{array}\right|=(-8+3)=-5$
    A32=(−1)3+2∣∣∣1034∣∣∣=−(4−0)=−4$A_{32}=(-1{)}^{3+2}\left|\begin{array}{ll}1& 3\\ 0& 4\end{array}\right|=-(4-0)=-4$
    A33=(−1)3+3∣∣∣10−2−1∣∣∣=(−1−0)=−1$A_{33}=(-1{)}^{3+3}\left|\begin{array}{cc}1& -2\\ 0& -1\end{array}\right|=(-1-0)=-1$
    Thus, adj A = ⎡⎣⎢A11A12A13A21A22A23A31A32A33⎤⎦⎥=⎡⎣⎢−9−8−2872−5−4−1⎤⎦⎥$\left[\begin{array}{lll}{A}_{11}& A_{21}& A_{31}\\ A_{12}& A_{22}& A_{32}\\ A_{13}& A_{23}& A_{33}\end{array}\right]=\left[\begin{array}{ccc}-9& 8& -5\\ -8& 7& -4\\ -2& 2& -1\end{array}\right]$
    Hence, A−1=1|A| adj A=11⎡⎣⎢−9−8−2872−5−4−1⎤⎦⎥$A^{-1}=\frac{1}{|A|}\text{ adj }A=\frac{1}{1}\left[\begin{array}{ccc}-9& 8& -5\\ -8& 7& -4\\ -2& 2& -1\end{array}\right]$
    Now, (A')-1 = (A-1)' = ⎡⎣⎢−9−8−2872−5−4−1⎤⎦⎥′=⎡⎣⎢−98−5−87−4−22−1⎤⎦⎥${\left[\begin{array}{ccc}-9& 8& -5\\ -8& 7& -4\\ -2& 2& -1\end{array}\right]}^{\prime }=\left[\begin{array}{ccc}-9& -8& -2\\ 8& 7& 2\\ -5& -4& -1\end{array}\right]$
16. |A|=2≠0$\left|A\right|=2\ne 0$
    Therefore A-1 exists
    AB = I
    A-1 AB = A-1I
    B = A-1
    adjA=[2143]$adjA=\left[\begin{array}{cc}2& 4\\ 1& 3\end{array}\right]$
    A−1=1|A|(adjA)$A^{-1}=\frac{1}{\left|A\right|}\left(adjA\right)$
    =12[2143]$=\frac{1}{2}\left[\begin{array}{cc}2& 4\\ 1& 3\end{array}\right]$
    =[112232]$=\left[\begin{array}{cc}1& 2\\ \frac{1}{2}& \frac{3}{2}\end{array}\right]$
    Hence B=[112232]$B=\left[\begin{array}{cc}1& 2\\ \frac{1}{2}& \frac{3}{2}\end{array}\right]$
17. According to the question,we have to use properties of determinants to prove that,
    ∣∣∣∣b+cq+ry+zc+ar+pz+xa+bp+qx+y∣∣∣∣=2∣∣∣∣apxbqycrz∣∣∣∣$\left|\begin{array}{ccc}b+c& c+a& a+b\\ q+r& r+p& p+q\\ y+z& z+x& x+y\end{array}\right|=2\left|\begin{array}{lll}a& b& c\\ p& q& r\\ x& y& z\end{array}\right|$
    Let LHS = ∣∣∣∣b+cq+ry+zc+ar+pz+xa+bp+qx+y∣∣∣∣$\left|\begin{array}{ccc}b+c& c+a& a+b\\ q+r& r+p& p+q\\ y+z& z+x& x+y\end{array}\right|$
    Therefore,on applying C1→$\to$ C1 + C2 + C3 we get,
    Δ=∣∣∣∣∣2(a+b+c)2(p+q+r)2(x+y+z)c+ar+pz+xa+bp+qx+y∣∣∣∣∣$\mathrm{\Delta }=\left|\begin{array}{ccc}2(a+b+c)& c+a& a+b\\ 2(p+q+r)& r+p& p+q\\ 2(x+y+z)& z+x& x+y\end{array}\right|$
    on taking 2 common from C1$C_1$,we get,
    Δ=2∣∣∣∣a+b+cp+q+rx+y+zc+ar+pz+xa+bp+qx+y∣∣∣∣$\mathrm{\Delta }=2\left|\begin{array}{ccc}a+b+c& c+a& a+b\\ p+q+r& r+p& p+q\\ x+y+z& z+x& x+y\end{array}\right|$
    On applying C2→$\to$ C2 - C1 and C3 →$\to$ C3 - C12,
    we get
    Δ=2∣∣∣∣a+b+cp+q+rx+y+z−b−q−y−c−r−z∣∣∣∣$\mathrm{\Delta }=2\left|\begin{array}{ccc}a+b+c& -b& -c\\ p+q+r& -q& -r\\ x+y+z& -y& -z\end{array}\right|$
    on applying C1→C1+C2+C3,we get,$C_1\to C_1+C_2+C_3,weget,$
    Δ=2∣∣∣∣apx−b−q−y−c−r−z∣∣∣∣$\mathrm{\Delta }=2\left|\begin{array}{ccc}a& -b& -c\\ p& -q& -r\\ x& -y& -z\end{array}\right|$
    ∴$\therefore$ Δ=2∣∣∣∣apxbqycrz∣∣∣∣$\mathrm{\Delta }=2\left|\begin{array}{lll}a& b& c\\ p& q& r\\ x& y& z\end{array}\right|$ [taking (-1) common from both C2 and C3]
    = RHS
18. x - y + z = 4
    x - 2y - 2z = 9
    2x + y + 3z = 1
    Let A=⎡⎣⎢112−1−211−23⎤⎦⎥X=⎡⎣⎢xyz⎤⎦⎥C=⎡⎣⎢491⎤⎦⎥$A=\left[\begin{array}{ccc}1& -1& 1\\ 1& -2& -2\\ 2& 1& 3\end{array}\right]X=\left[\begin{array}{c}x\\ y\\ z\end{array}\right]C=\left[\begin{array}{c}4\\ 9\\ 1\end{array}\right]$
    AX = C
    AB=⎡⎣⎢112−1−211−23⎤⎦⎥⎡⎣⎢−4−7541−343−1⎤⎦⎥$AB=\left[\begin{array}{ccc}1& -1& 1\\ 1& -2& -2\\ 2& 1& 3\end{array}\right]\left[\begin{array}{ccc}-4& 4& 4\\ -7& 1& 3\\ 5& -3& -1\end{array}\right]$ =⎡⎣⎢800080008⎤⎦⎥$=\left[\begin{array}{ccc}8& 0& 0\\ 0& 8& 0\\ 0& 0& 8\end{array}\right]$
    AB = 8I
    A−1=18B[∵A−1AB=8A−1IB=8A−1]$A^{-1}=\frac{1}{8}B\left[\begin{array}{c}\because A^{-1}AB=8A^{-1}I\\ B=8A^{-1}\end{array}\right]$
    =18⎡⎣⎢−4−7541−343−1⎤⎦⎥$=\frac{1}{8}\left[\begin{array}{ccc}-4& 4& 4\\ -7& 1& 3\\ 5& -3& -1\end{array}\right]$
    X = A-1C
    ⎡⎣⎢xyz⎤⎦⎥=⎡⎣⎢3−2−1⎤⎦⎥$\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{c}3\\ -2\\ -1\end{array}\right]$
    x = 3, y = -2, z = -1