Differential Equations - Exemplar Solutions
CBSE Class–12 Mathematics
NCERT Exemplar
Chapter - 9
DIFFERENTIAL EQUATIONS - Short Answer Questions
1. Find the differential equation of the family of curves 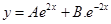 .
.
Sol. Given 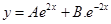 .
.
Differentiating on both sides with respect to x
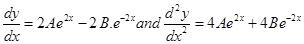
Thus, 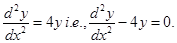
2. Find the general solution of the differential equation 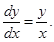
Sol.Given 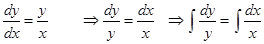
(Using formula logA +logB=logAB in RHS and removing log on both sides)
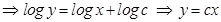
3. Given that 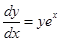 and
and 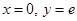 . Find the value of
. Find the value of 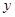 when
when 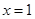 .
.
Sol. Given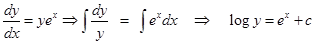
Substituting 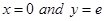 we get
we get 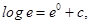 i.e.,
i.e., 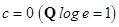
Therefore, 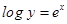 .
.
Now, substituting x = 1 in the above, we get 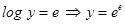 .
.
4. Solve the differential equation 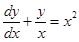
Sol. The equation is of the type 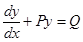 , which is a linear differential equation.
, which is a linear differential equation.
Now I.F. 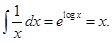 (elogf(x)=f(x))
(elogf(x)=f(x))
Therefore, solution of the given differential equation is
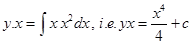
Hence, 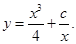
5. Find the differential equation of the family of lines through the origin.
Sol. Let 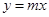 be the family of lines through origin. Therefore,
be the family of lines through origin. Therefore, 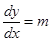 .
.
Eliminating m, we get 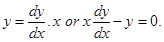
6. Find the differential equation of all non-horizontal lines in a plane.
Sol. The general equation of all non-horizontal lines in a plane is 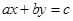 , where
, where 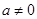 .
.
differentiating both sides w.r.t. y on both sides,we get
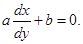
Again, differentiating both sides w.r.t. y, we get
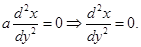
7. Find the equation of a curve whose tangent at any point on it, different from origin, has slope 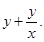
Sol. Given 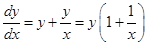
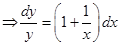
Integrating on both sides, we get
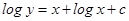
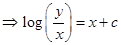
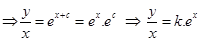
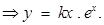
8. Find the equation of a curve which is passing through the point (1, 1).If the perpendicular distance of the origin from the normal at any point  of the curve is equal to the distance of P form the
of the curve is equal to the distance of P form the 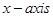 .
.
Sol. Let the equation of normal at 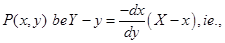
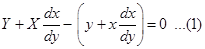
Therefore, the length of perpendicular from origin to (1) is 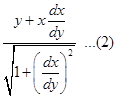
Also, distance between 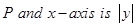 . Thus, we get
. Thus, we get
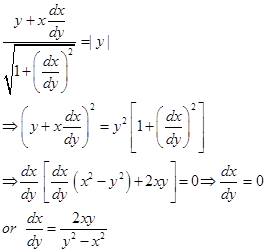
Case I: 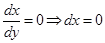
Integrating both sides, we get 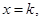 Substituting
Substituting 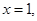 we get
we get 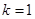 .
.
Therefore, 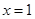 is the equation of curve (not possible, so rejected).
is the equation of curve (not possible, so rejected).
Case II: 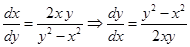 . Substituting
. Substituting 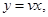 we get
we get
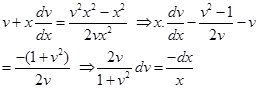
Integrating both sides, we get
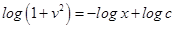
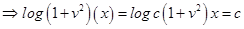
 Substituting
Substituting 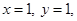 we get
we get 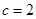 .
.
Therefore, 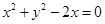 is the required equation.
is the required equation.
9. Find the equation of a curve passing through 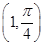 .If the slope of the tangent to the curve at any point
.If the slope of the tangent to the curve at any point  is
is 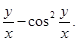
Sol. According to the given condition
slope of tangent,m=dy/dx
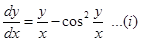
This is a homogeneous differential equation. Substituting 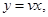 we get
we get
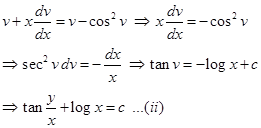
Substituting 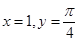 , we get
, we get 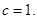 Thus, we get
Thus, we get
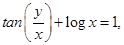 which is the required equation.
which is the required equation.
10. Solve 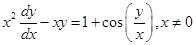 and
and 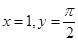
Sol. Given equation can be written as
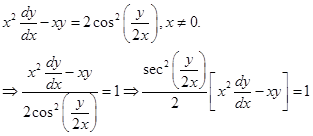
Dividing both sides by 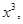 we get
we get
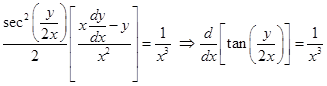
Integrating both sides, we get
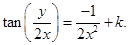
Substituting 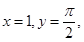 we get
we get
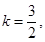 therefore,
therefore, 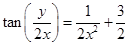 is the required solution.
is the required solution.
11. State the type of the differential equation for the equation. 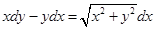 and solve it.
and solve it.
Sol. Given equation can be written as 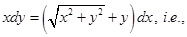
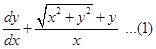
Clearly RHS of (1) is a homogeneous function of degree zero. Therefore, the given equation is a homogeneous differential equation. Substituting 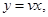 we get form (1)
we get form (1)
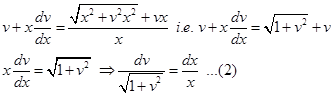
Integrating both sides of (2), we get
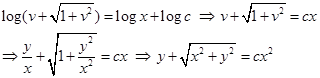
Choose the correct answer form the given four options in each of the Examples 12 to 21.
12. The degree of the differential equation 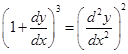 is
is
(A) 1
(B) 2
(C) 3
(D) 4
Sol. The correct answer is (B).
13. The degree of the differential equation 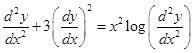 is
is
(A) 1
(B) 2
(C) 3
(D) Not defined
Sol. Correct answer is (D). The given differential equation is not a polynomial equation in terms of its derivatives, so its degree is not defined.
14. The order and degree of the differential equation 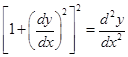 respectively, are
respectively, are
(A) 1, 2
(B) 2, 2
(C) 2, 1
(D) 4, 2
Sol. Correct answer is (C).
15. The order of the differential equation of all circles of given radius 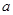 is:
is:
(A) 1
(B) 2
(C) 3
(D) 4
Sol. Correct answer is (B). Let the equation of given family be 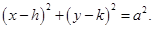 It has two arbitrary constants h and k. Therefore, the order of the given differential equation will be 2.
It has two arbitrary constants h and k. Therefore, the order of the given differential equation will be 2.
16. The solution of the differential equation 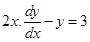 represents a family of
represents a family of
(A) straight lines
(B) circles
(C) parabolas
(D) ellipses
Sol. Correct answer is (C). Given equation can be written as
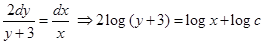
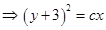 which represents the family of parabolas.
which represents the family of parabolas.
17. The integrating factor of the differential equation
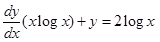 is
is
(A) 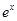
(B) 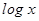
(C) 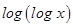
(D) 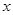
Sol. Correct answer is (B). Given equation can be written as 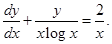
Therefore, I.F. 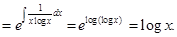
18. A solution of the differential equation 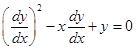 is
is
(A) 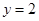
(B) 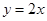
(C) 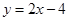
(D) 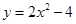
Sol. Correct answer is (C).
19. Which of the following is not a homogeneous function of 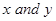 .
.
(A) 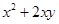
(B) 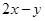
(C) 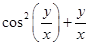
(D) 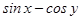
Sol. Correct answer is (D).
20. Solution of the differential equation 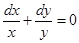 is
is
(A) 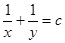
(B) 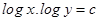
(C) 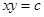
(D) 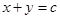
Sol. Correct answer is (C). From the given equation, we get 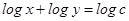 giving
giving 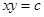 .
.
21. The solution of the differential equation 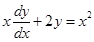 is
is
(A) 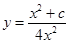
(B) 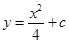
(C) 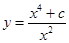
(D) 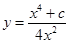
Sol. Correct answer (D). 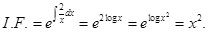 Therefore, the solution is
Therefore, the solution is
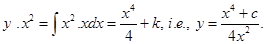
22. Fill in the blanks of the following:
(i) Order of the differential equation representing the family of parabolas 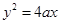 is ____________.
is ____________.
Sol. One; a is the only arbitrary constant.
(ii) The degree of the differential equation 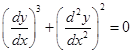 is _______________.
is _______________.
Sol. Two; since the degree of the highest order derivative is two.
(iii) The number of arbitrary constants in a particular solution of the differential equation 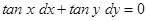 is _______________.
is _______________.
Sol. Zero; any particular solution of a differential equation has no arbitrary constant.
(iv) 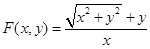 is a homogeneous function of degree _________________.
is a homogeneous function of degree _________________.
Sol. Zero.
(v) An appropriate substitution to solve the differential equation 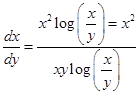 is ________.
is ________.
Sol. 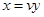 .
.
(vi) Integrating factor of the differential equation 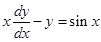 is ______________.
is ______________.
Sol. 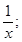 given differential equation can be written as
given differential equation can be written as 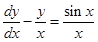 and therefore
and therefore 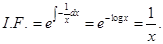
(vii) The general solution of the differential equation 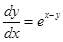 is _______________.
is _______________.
Sol. 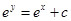 from given equation, we have
from given equation, we have 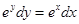 .
.
(viii) The general solution of the differential equation  is ______________.
is ______________.
Sol. 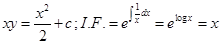 and the solution is
and the solution is 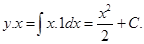
(ix) The differential equation representing the family of curves 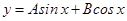 is ____________.
is ____________.
Sol. 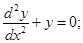 Differentiating the given function w.r.t. x successively, we get
Differentiating the given function w.r.t. x successively, we get
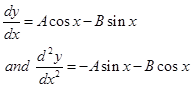
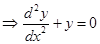 is the differential equation.
is the differential equation.
(x) 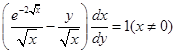 when written in the form
when written in the form 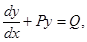 then P = _______________.
then P = _______________.
Sol. 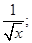 the given equation can be written as
the given equation can be written as
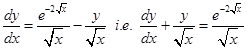
This is a differential equation of the type 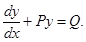
23. State whether the following statements are True or False.
(i) Order of the differential equation representing the family of ellipses having centre at origin and foci on x-axis is two.
Sol. True, since the equation represents the given family 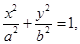 which has two arbitrary constants.
which has two arbitrary constants.
(ii) Degree of the differential equation 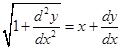 is not defined.
is not defined.
Sol. True, because it is not a polynomial equation in its derivatives.
(iii) 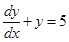 is a differential equation of the type
is a differential equation of the type 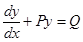 but it can be solved using variable separable method also.
but it can be solved using variable separable method also.
Sol. True
(iv) 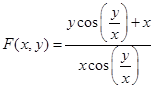 is not a homogeneous function.
is not a homogeneous function.
Sol. True, because 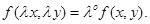
(v) 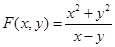 is a homogeneous function of degree 1.
is a homogeneous function of degree 1.
Sol. True, because 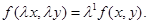
(vi) Integrating factor of the differential equation 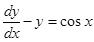 is
is 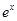 .
.
Sol. False, because I.F 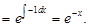
(vii) The general solution of the differential equation  is
is 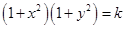 .
.
Sol. True, because given equation can be written as
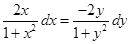
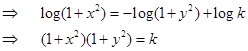
(viii) The general solution of the differential equation 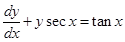 is
is 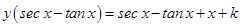 .
.
Sol. False, since I.F. 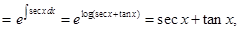 the solution is,
the solution is,
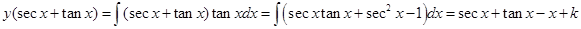
(ix) 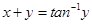 is a solution of the differential equation
is a solution of the differential equation 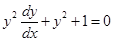
Sol. True, 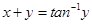
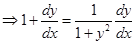
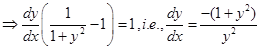 which satisfies the given equation.
which satisfies the given equation.
(x) 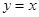 is a particular solution of the differential equation
is a particular solution of the differential equation 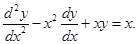
Sol. False, 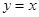 because does not satisfy the given differential equation.
because does not satisfy the given differential equation.