Integrals - Exemplar Solutions
CBSE Class–12 Mathematics
NCERT Exemplar
Chapter - 7
INTEGRALS - Short Answer Questions
1. Integrate 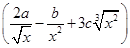 w.r.t. x
w.r.t. x
Sol. 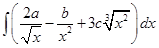
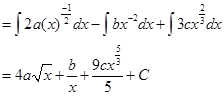
2. Evaluate 
Sol. Let then 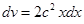
Therefore, 

3. Verify the following using the concept of integration as an antiderivative.
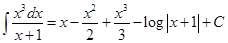
Sol. 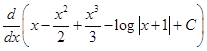

Thus 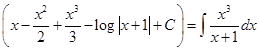
4. Evaluate 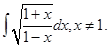
Sol. Let 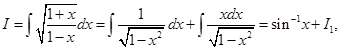
where 
Put 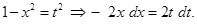 Therefore
Therefore

Hence 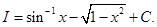
5. Evaluate  .
.
Sol. Put 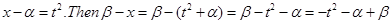 and
and  . Now
. Now
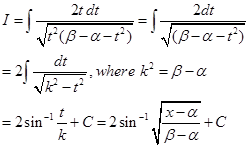
6. Evaluate 
Sol. 
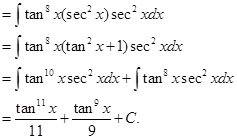
7. Find
Sol. Put 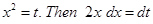 .
.
Now 
Consider 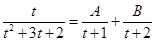
Comparing coefficient, we get 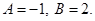
Then 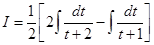
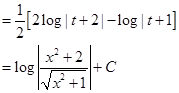
8. Find 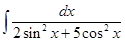
Sol. Dividing numerator and denominator by 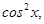 we have
we have
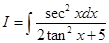
Put  so that
so that 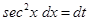 . Then
. Then
=
9. Evaluate  as a limit of sums.
as a limit of sums.
Sol. Here  and
and  i.e,
i.e, 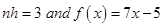 .
.
Now, we have
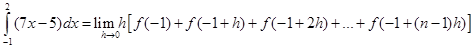
Now that

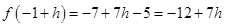
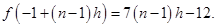
Therefore,
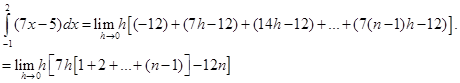
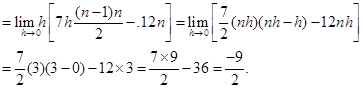
10. Evaluate 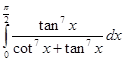
Sol. We have

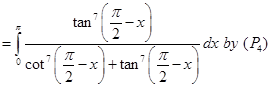
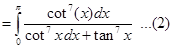
Adding (1) and (2), we get
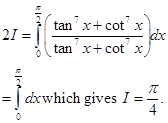
11. Find 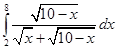
Sol. We have

....(2)
Adding (1) and (2), we get:
12. Find 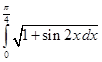
Sol. We have

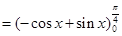
I = 1.
13. Find 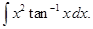
Sol. 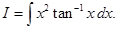

14. Find 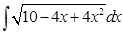
Sol. We have
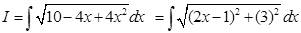
Put 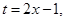 then
then 
Therefore, 
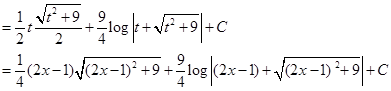
15. Evaluate 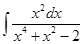 .
.
Sol. Let 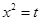 . Then
. Then
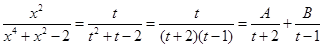
So 
Comparing coefficients, we get 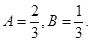
So 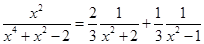
Therefore,
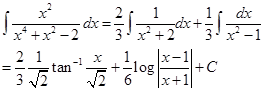
16. Evaluate 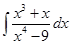
Sol. we have
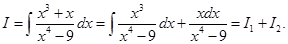
Now 
Put 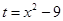 so that
so that 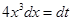 . Therefore
. Therefore

Again, 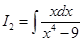
Put 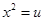 so that
so that 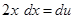 . Then
. Then

Thus 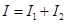
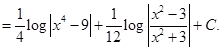
17. Show that 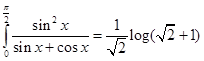
Sol. We have



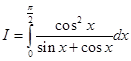
Thus, we get 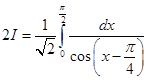
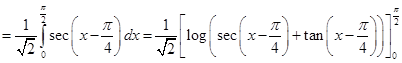
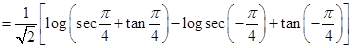
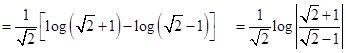
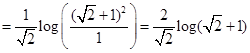
Hence, 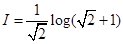
18. Find 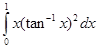
Sol. 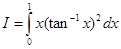
Integrating by parts, we have
Now 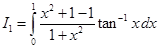
where
Thus,
Therefore,
19. Evaluate 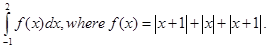
Sol. We can redefine 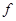 as
as 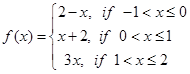
Therefore, 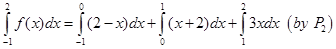
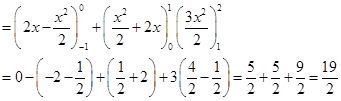
Choose the correct answer from the given four options in each of the Examples from 20 to 30.
20. 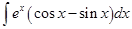 is equal to
is equal to
(A) 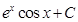
(B) 
(C) 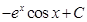
(D) 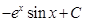
Sol. (A) is the correct answer since
. Here  .
.
So, 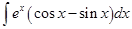 =
=
21. 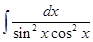 is equal to
is equal to
(A) 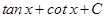
(B) 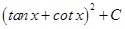
(C) 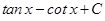
(D) 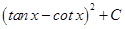
Sol. (C) is the correct answer, since
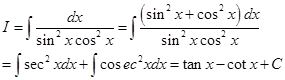
22. If 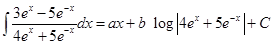 , then
, then
(A) 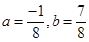
(B) 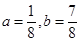
(C) 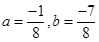
(D) 
Sol. (C) is the correct answer, since differentiating both sides, we have
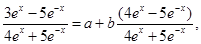
Giving 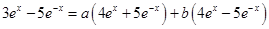 . Comparing coefficients on both sides, we get
. Comparing coefficients on both sides, we get
 . This verifies
. This verifies 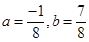
23. 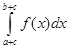 is equal to
is equal to
(A) 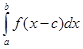
(B) 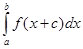
(C) 
(D) 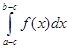
Sol. (B) is the correct answer, since by putting 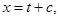 we get
we get
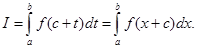
24. If  are continuous in [0, 1] satisfying
are continuous in [0, 1] satisfying  and
and 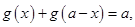 then
then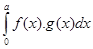 then is equal to
then is equal to
(A) 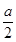
(B) 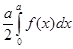
(C) 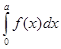
(D) 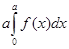
Sol. (B) is the correct answer. Since 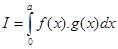
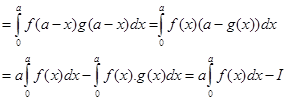
Or 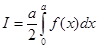
25. then 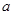 is equal to
is equal to
(A) 3
(B) 6
(C) 9
(D) 1
Sol. (C) is the correct answer, since
which gives 
So, a = 9
26. 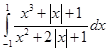 is equal to
is equal to
(A) log 2
(B) 2 log 2
(C) 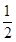 log 2
log 2
(D) 4 log 2
Sol. (B) is the correct answer, since 
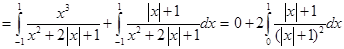
[odd function + even function]
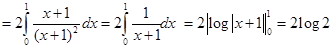
27. If 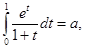 then
then 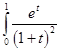 is equal to
is equal to
(A) 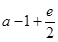
(B) 
(C) 
(D) 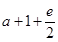
Sol. (B) is the correct answer, since 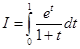
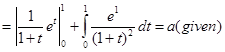
Therefore, 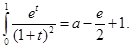
28. 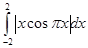 is equal to
is equal to
(A) 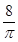
(B) 
(C) 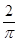
(D) 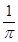
Sol. (A) is the correct answer, since 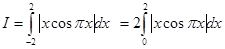
 (Since)
(Since)
Fill in the blanks in each of the Examples 29 to 32.
29. 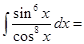 ______________.
______________.
Sol. Since,
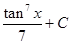
30. 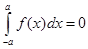 if
if 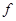 is an ______________ function.
is an ______________ function.
Sol. Odd.
31. 
Sol. 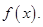
32.  _________________.
_________________.
Sol.  .
.