Integrals - Revision Notes

 CBSE Class 12 Mathematics

Chapter-7
Integrals

---

• Integration is the inverse process of differentiation. In the differential calculus, we are given a function and we have to find the derivative or differential of this function, but in the integral calculus, we are to find a function whose differential is given. Thus, integration is a process which is the inverse of differentiation. Let 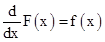. Then we write 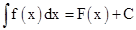. These integrals are called indefinite integrals or general integrals, C is called constant of integration. All these integrals differ by a constant.
• From the geometric point of view, an indefinite integral is collection of family of curves, each of which is obtained by translating one of the curves parallel to itself upwards or downwards along the y-axis.
• Some properties of indefinite integrals are as follows:

1. ∫[f(x)+g(x)]dx=∫f(x)dx+∫g(x)dx$\int \left[f\left(x\right)+g\left(x\right)\right]dx=\int f\left(x\right)dx+\int g\left(x\right)dx$

2. For any real number k,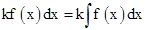 

More generally, if 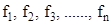 are functions and  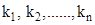are real numbers. Then

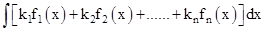
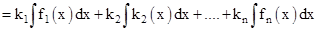
• Some standard integrals:

(i) 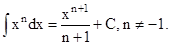      Particularly,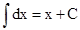 

(ii)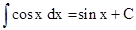         

(iii)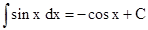      

(iv)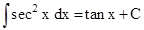       

(v)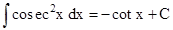         

(vi)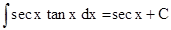       

(vii)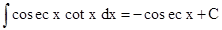     

(viii)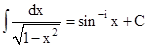       

(ix)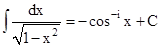       

(x)    ∫dx1+x2=tan−1x+C$\int \frac{dx}{1+x^2}=ta{n}^{-1}x+C$
(xi)       ∫dx1+x2=−cot−1x+C$\int \frac{dx}{1+x^2}=-co{t}^{-1}x+C$

(xii)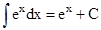     

(xiii)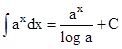   

(xiv)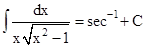   

(xv)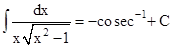     

(xvi)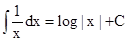   

• Integration by Partial Fraction: A rational fraction is the ratio of the form P(x)Q(x)$\frac{\mathrm{P}\left(x\right)}{\mathrm{Q}\left(x\right)}$ where P(x) and Q(x) are polynomials in x and Q(x) ≠$\ne$ 0. If the degree of the polynomial P(x) is greater than the degree of the polynomial Q(x), then we may divide P(x) by Q(x) so that P(x)Q(x)=T(x)+P1(x)Q(x)$\frac{\mathrm{P}\left(x\right)}{\mathrm{Q}\left(x\right)}=\mathrm{T}\left(x\right)+\frac{{\mathrm{P}}_1\left(x\right)}{\mathrm{Q}\left(x\right)}$ where T(x) is a polynomial in x and degree of P1(x) is less than Q(x). T(x) is a polynomial can be easily integrated.

P1(x)Q(x)$\frac{{\mathrm{P}}_1\left(x\right)}{\mathrm{Q}\left(x\right)}$can be integrated by expressing P1(x)Q(x)$\frac{{\mathrm{P}}_1\left(x\right)}{\mathrm{Q}\left(x\right)}$ as the sum of partial fractions of the following types:

(a) px+q(x−a)(x−b)=Ax−a+Bx−b$\frac{px+q}{\left(x-a\right)\left(x-b\right)}=\frac{\mathrm{A}}{x-a}+\frac{\mathrm{B}}{x-b}$ x≠a,x≠b,a≠b$x\ne a,x\ne b,a\ne b$

(b) px+q(x−a)2=Ax−a+B(x−a)2$\frac{px+q}{{\left(x-a\right)}^2}=\frac{\mathrm{A}}{x-a}+\frac{\mathrm{B}}{{\left(x-a\right)}^2}$

(c) px2+qx+r(x−a)(x−b)(x−c)=Ax−a+Bx−b+Cx−c$\frac{p{x}^2+qx+r}{\left(x-a\right)\left(x-b\right)\left(x-c\right)}=\frac{\mathrm{A}}{x-a}+\frac{\mathrm{B}}{x-b}+\frac{\mathrm{C}}{x-c}$

(d) px2+qx+r(x−a)2(x−b)=Ax−a+B(x−a)2+Cx−b$\frac{p{x}^2+qx+r}{{\left(x-a\right)}^2\left(x-b\right)}=\frac{\mathrm{A}}{x-a}+\frac{\mathrm{B}}{{\left(x-a\right)}^2}+\frac{\mathrm{C}}{x-b}$

(e) px2+qx+r(x−a)(x2+bx+c)=Ax−a+Bx+Cx2+bx+c$\frac{p{x}^2+qx+r}{\left(x-a\right)\left(x^2+bx+c\right)}=\frac{\mathrm{A}}{x-a}+\frac{\mathrm{B}x+\mathrm{C}}{x^2+bx+c}$ where x2+bx+c$x^2+bx+c$ cannot be factorize further into linear fraction.

• Integration by Substitution: In this method we change the variable to some other variable. When the integrand involves some trigonometric functions, we shall be using some well-known identities to find the integrals. Using substitution technique, we obtain the following standard integrals:

(a) ∫tanxdx=log|secx|+c$\int \tan xdx=\log \left|\sec x\right|+c$

(b) ∫cotxdx=log|sinx|+c$\int \cot xdx=\log \left|\sin x\right|+c$

(c) ∫secxdx=log|secx+tanx|+c$\int \sec xdx=\log \left|\sec x+\tan x\right|+c$

(d) ∫cosecxdx=log|cosecx−cotx|+c$\int \cos ecxdx=\log \left|\cos ecx-\cot x\right|+c$

• Integrals of Some Special Functions:

(a) ∫dxx2−a2=12alog∣∣x−ax+a∣∣+c$\int \frac{dx}{x^2-a^2}=\frac{1}{2a}\log \left|\frac{x-a}{x+a}\right|+c$                    (b) ∫dxa2−x2=12alog∣∣a+xa−x∣∣+c$\int \frac{dx}{a^2-x^2}=\frac{1}{2a}\log \left|\frac{a+x}{a-x}\right|+c$

(c) ∫dxx2+a2=1atan−1xa+c$\int \frac{dx}{x^2+a^2}=\frac{1}{a}{\tan }^{-1}\frac{x}{a}+c$                               (d) ∫dxx2−a2√=log∣∣x+x2−a2−−−−−−√∣∣+c$\int \frac{dx}{\sqrt{x^2-a^2}}=\log \left|x+\sqrt{x^2-a^2}\right|+c$

(e) ∫dxa2+x2√=log∣∣x+a2+x2−−−−−−√∣∣+c$\int \frac{dx}{\sqrt{a^2+x^2}}=\log \left|x+\sqrt{a^2+x^2}\right|+c$               (f)  ∫dxa2−x2√=sin−1xa+c$\int \frac{dx}{\sqrt{a^2-x^2}}={\sin }^{-1}\frac{x}{a}+c$

• Integration by Parts: For the given function f(x) and g(x),

                        ∫f(x).g(x)dx=f(x)∫g(x)dx−∫{f′(x)∫g(x)dx}dx$\int f\left(x\right).g\left(x\right)dx=f\left(x\right)\int g\left(x\right)dx-\int \left\{f^{\prime }\left(x\right)\int g\left(x\right)dx\right\}dx$

We must take proper care to choose the first function and second function clearly. We must choose that function as the second function whose integral is well-known to us.

• ∫ex[f(x)+f′(x)]dx=exf(x)+c$\int e^x\left[f\left(x\right)+f^{\prime }\left(x\right)\right]dx=e^{x}f\left(x\right)+c$
• Some Special Type of Integrals:

(a) ∫a2−x2−−−−−−√dx=12[xa2−x2−−−−−−√+a2sinxa]$\int \sqrt{a^2-x^2}dx=\frac{1}{2}\left[x\sqrt{a^2-x^2}+a^2\sin \frac{x}{a}\right]$

(b) ∫x2+a2−−−−−−√dx=12[xx2+a2−−−−−−√+a2log∣∣x+x2+a2−−−−−−√∣∣]+c$\int \sqrt{x^2+a^2}dx=\frac{1}{2}\left[x\sqrt{x^2+a^2}+a^2\log \left|x+\sqrt{x^2+a^2}\right|\right]+c$

(c) ∫x2−a2−−−−−−√dx=12[xx2−a2−−−−−−√+a2log∣∣x+x2−a2−−−−−−√∣∣]+c$\int \sqrt{x^2-a^2}dx=\frac{1}{2}\left[x\sqrt{x^2-a^2}+a^2\log \left|x+\sqrt{x^2-a^2}\right|\right]+c$

• Integrals of the types ∫dxax2+bx+c$\int \frac{dx}{a{x}^2+bx+c}$ or ∫dxax2+bx+c√$\int \frac{dx}{\sqrt{a{x}^2+bx+c}}$

(a) These type of integrals are transformed into standard form by expressing

      ax2+bx+c=a(x2+bxa+ca)=a[(x+b2a)2+(ca−b24a2)]$a{x}^2+bx+c=a\left(x^2+\frac{bx}{a}+\frac{c}{a}\right)=a\left[{\left(x+\frac{b}{2a}\right)}^2+\left(\frac{c}{a}-\frac{b^2}{4a^2}\right)\right]$

(b) Integrals of the types ∫px+qax2+bx+cdx$\int \frac{px+q}{a{x}^2+bx+c}dx$ or ∫px+qax2+bx+c√dx$\int \frac{px+q}{\sqrt{a{x}^2+bx+c}}dx$ are transformed into standard form by expressing px+d=Addx(ax2+bx+c)+B$px+d=\mathrm{A}\frac{d}{dx}\left(a{x}^2+bx+c\right)+\mathrm{B}$

⇒$\Rightarrow$          px+d=A(2ax+b)+B$px+d=\mathrm{A}\left(2ax+b\right)+\mathrm{B}$

where A abd B are determined by comparing coefficients on both sides.

• We have already defined ∫abf(x)dx$\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ as the area of the region bounded by the curve y=f(x)$y=f\left(x\right)$, a≤x≤b,$a\le x\le b,$ the x-axis and the ordinates x = a and x = b. Let x be a given point in [a, b], then ∫abf(x)dx$\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ represents the area function A(x).
• First Fundamental Theorem of Integral Calculus: Let the area function be defined by A(x)=∫abf(x)dx$\mathrm{A}\left(x\right)=\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ for all x≥a$x\ge a$ where the function f is assumed to be continuous on [a, b], then A′(x)=f(x)${\mathrm{A}}^{\prime }\left(x\right)=f\left(x\right)$ for all x∈[a,b]$x\in \left[a,b\right]$.
• Secind Fundamental Theorem of Integral Calculus: Let f be a continuous function of x defined on the closed interval ]a, b] and let F be another function such that ddxF(x)=f(x)$\frac{d}{dx}\mathrm{F}\left(x\right)=f\left(x\right)$ for all x in the domain of f, then ∫abf(x)dx=F(x)+C]ba=F(b)−F(a)$\underset{a}{\overset{b}{\int }}f\left(x\right)dx=\mathrm{F}\left(x\right)+{\mathrm{C}]}_a^b=\mathrm{F}\left(b\right)-\mathrm{F}\left(a\right)$

This is called the definite integral of f over the range [a, b] were a and b are called the limits of integration, a$a$ being the lower limit and b$b$ the upper limit.