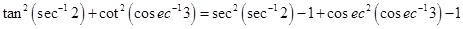Inverse Trigonometric Functions - Exemplar Solutions
CBSE Class–12 Mathematics
NCERT Exemplar
Chapter - 2
Inverse Trigonometric Functions - Short Answer Questions
1. Find the principal value of cos–1x, for 
.
Sol.If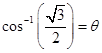 
, then 
.
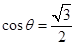Since we are considering principal branch,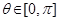 
. Also, since
, 
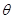being in the first quadrant, hence 
2. Evaluate
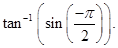
Sol.
=
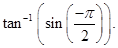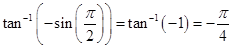
3. Find the value of
Sol.
4. Find the value of
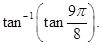
Sol.
.
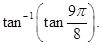
5. Evaluate
.
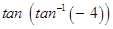Sol.Since
6. Evaluate:
.
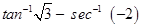Sol.
= 
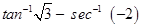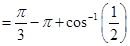
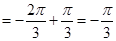
7. Evaluate:
.
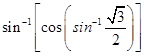Sol.
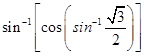
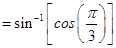
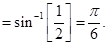
8. Prove that 
. State with reason whether the equality is valid for all values of x.
Sol.Let 
Or,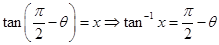 
So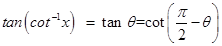 
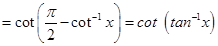
The equality is valid for all values of x since tan–1x and cot–1x are true for x 
R.
9. Find the value of
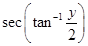
Sol.Let
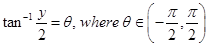. So,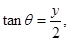 
which gives 
.
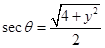Therefore, 
.
10. Find value of tan (cos–1x) and hence evaluate
Sol.Let 
then 
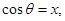where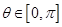 
Therefore,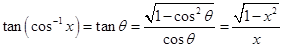 
Hence,
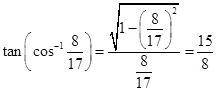
11. Find the value of
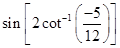
Sol.Let
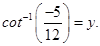Then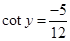 
.
Now
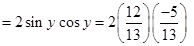
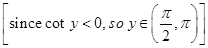
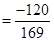
12. Evaluate
Sol.
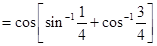
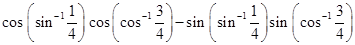
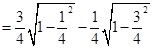
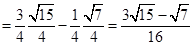
Long Answer Questions
13. Prove that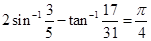 
Sol.Let
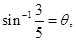
then
where
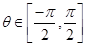
Thus
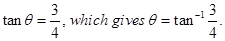
Therefore,
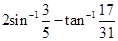
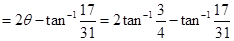
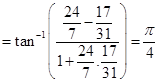
14. Prove that 
Sol.We have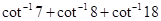
=
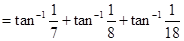
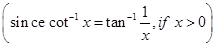
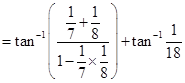
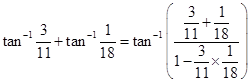
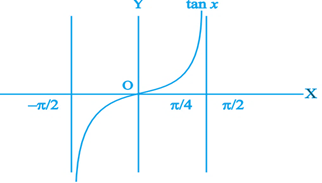
15. Which is greater, tan 1 or tan–1 1?
Sol.From Fig. we note that tan x is an increasing function in the interval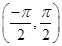 
, since 
This gives
tan 1>1
16. Find the value of
Sol. Let
and
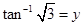
so that
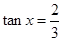and
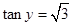
Therefore,
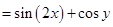
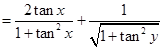
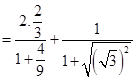
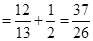
17. Solve for x
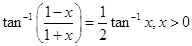
Sol.From given equation, we have
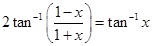
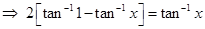
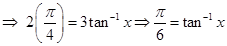
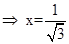
18. Find the values of x which satisfy the equation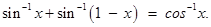 
Sol.From the given equation, we have
+
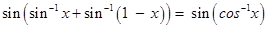
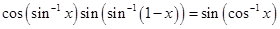
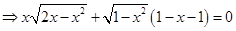
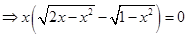
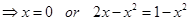
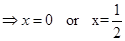
19. Solve the equation
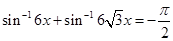
Sol.From the given equation, we have
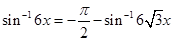
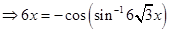
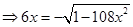. Squaring, we get
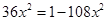
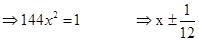
Note that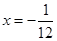 
is the only root of the equation as 
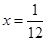does not satisfy it.
20. Show that
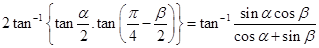
Sol.L.H.S. =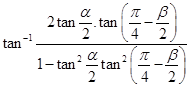
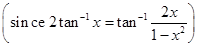
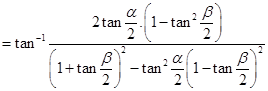
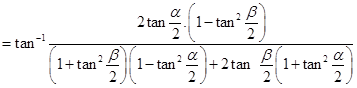
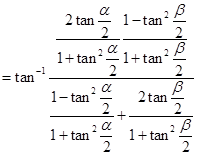
Choose the correct answer from the given four options in each of 21 to 41.
21. Which of the following corresponds to the principal value branch of tan–1?
(A)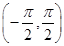 
(B)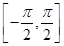 
(C) 
(D) 
Sol.(A) is the correct answer.
22. The principal value branch of sec-1is
(A)
(B) 
(C) (0, π)
(D)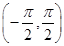
Sol.(B) is the correct answer.
23. One branch of cos–1 other than the principal value branch corresponds to
(A)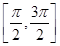 
(B)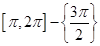 
(C) (0, π)
(D) [2π, 3π]
Sol.(D) is the correct answer.
24. The value of
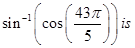
(A)
(B)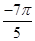 
(C)
(D)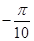 
Sol.(D) is the correct answer.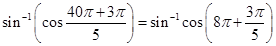 
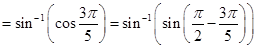
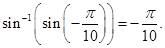
25. The principal value of the expression
(A)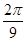
(B)
(C)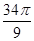
(D)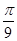
Sol.(A) is the correct answer. Cos-1(cos (680°)) = cos-1[cos (720° – 40°)]
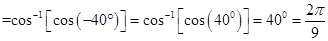
26. The value of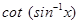 
is
(A) 
(B) 
(C)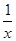 
(D)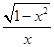 
Sol.(D) is the correct answer. Let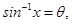 
then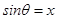 
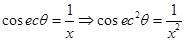
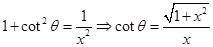
27. If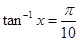 
for some 
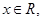then the value of 
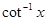is
(A)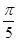 
(B)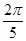 
(C)
(D)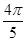 
Sol.(B) is the correct answer. We know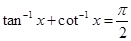 
. Therefore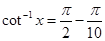 
28. The domain of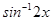 
is
(A) [0, 1]
(B) [– 1, 1]
(C)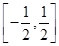 
(d)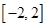 
Sol.(C) is the correct answer. Let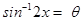 
so that
.
Now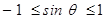 
, i.e., 
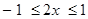which gives
.
29. The principal value of 
is
(A)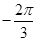 
(B)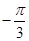 
(C)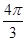 
(D) 
Sol.(B) is the correct answer.
30. The greatest and least values of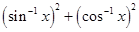 
are respectively
(A) 
(B)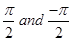 
(C)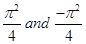 
(D)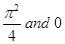 
Sol.(A) is the correct answer. We have
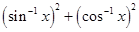
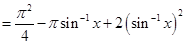
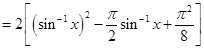
Thus, the least value is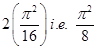 
and the Greatest value is 
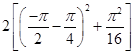, i.e.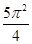
31. Let , then value of 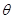is
(A) 
(B)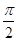 
(C)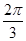 
(D)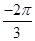 
Sol.(A) is the correct answer.
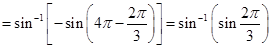
32. The domain of the function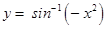 
is
(A) [0, 1]
(B) (0, 1)
(C) [–1, 1]
(D)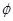 
Sol.(C) is the correct answer. 
i.e. – 1 ≤– x2 ≤1 (since – 1 ≤sin y ≤1)
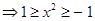
33. The domain of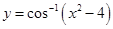 
is
(A) [3, 5]
(B) [0, π]
(C)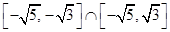 
(D) 
Sol.(D) is the correct answer.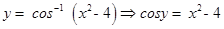 
i.e. 
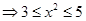
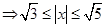
34. The domain of the function defined by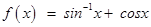 
is
(A) [–1, 1]
(B) [–1, π + 1]
(C)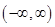 
(D)
Sol.(A) is the correct answer. The domain of cos is R and the domain of sin–1 is [–1, 1]. Therefore, the domain of 
i.e. 
35. The value of sin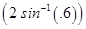 
is
(A) .48
(B) .96
(C) 1.2
(D) sin 1.2
Sol.(B) is the correct answer. Let sin-1 (.6) = θ, i.e., sin θ= .6.
Now sin (2θ) = 2 sinθ cosθ= 2 (.6) (.8) = .96.
36. If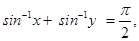 
then value of 
is
(A)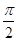
(B) π
(C) 0
(D)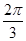
Sol.(A) is the correct answer. Given that 
Therefore,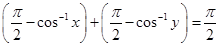 
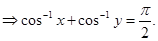
37. The value of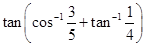 
is
(A) 
(B) 
(C) 
(D)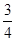 
Sol.(A) is the correct answer.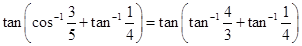 
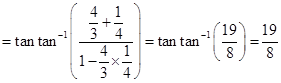
38. The value of the expression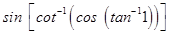 
is
(A) 0
(B) 1
(C) 
(D)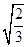 
Sol.(D) is the correct answer.
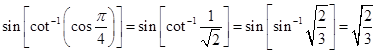
39 The equation 
has
(A) no Solution
(B) unique Solution
(C) infinite number of Solutions
(D) two Solutions
Sol.(B) is the correct answer. We have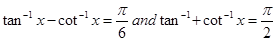 
Adding them, we get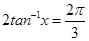 
40. If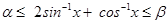 
, then
(A)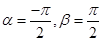 
(B)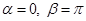 
(C) 
(D)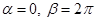 
Sol.(B) is the correct answer. We have
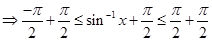
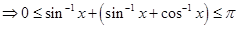
41. The value of tan 
is
(A) 5
(B) 11
(C) 13
(D) 15
Sol.(B) is the correct answer.
