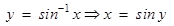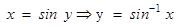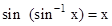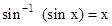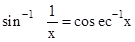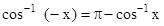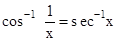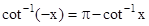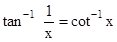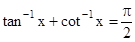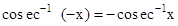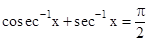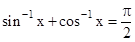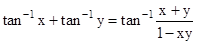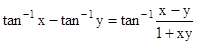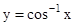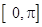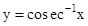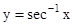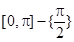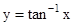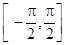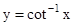CBSE Class 12 Mathematics
Chapter-02
Inverse Trigonometric Functions
- The domains and ranges (principal value branches) of inverse trigonometric functions are given in the following table:
Functions | Domain | Range (Principal Value Branches) |
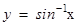
| [-1, 1] | 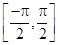
|
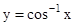
| [-1, 1] | 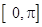
|
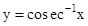
| R- [-1, 1] | 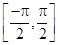 - {0} - {0}
|
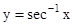
| R-[-1, 1] | 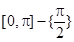
|
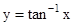
| R | 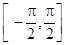
|
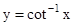
| R | 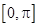
|
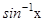 should not be confused with
should not be confused with 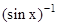 . In fact
. In fact 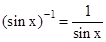 And similarly for other trigonometric functions.
And similarly for other trigonometric functions.- The value of an inverse trigonometric functions which lies in its principal value branch is called the principal value of that inverse trigonometric functions.
- For suitable values of domain, we have
• 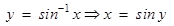
• 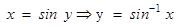
• 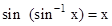
• 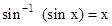
• 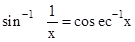
• 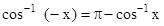
• 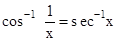
• 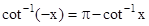
• 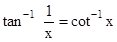
cot−11x=tan−1x
cosec−11x=sin−1x
• 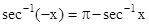
sec−11x=cos−1x
• 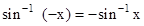
• 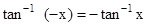
• 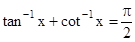
• 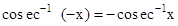
• 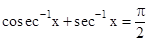
• 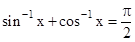
sin−1x+sin−1y=sin−1(x1−y2−−−−−√+y1−x2−−−−−√)
cos−1x+ocos−1y=cos−1(xy−1−x2−−−−−√1−y2−−−−−√)
• 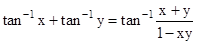
• 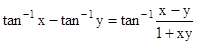
tan−1x+tan−1y+tan−1z = tan−1(x+y+z−xyz1−xy−yz−zx)
2sin−1x=sin−1(2x1−x2−−−−−√)
2cos−1x=cos−1(2x2−1)
• 2tan−1x=sin−1(2x1+x2) = cos−1(1−x21+x2)=tan−1(2x1−x√)
3sin−1x=sin−1(3x−4x3)
3cos−1x=cos−1(4x3−3x)
3tan−1x=tan−1(3x−x31−3x2)
Conversion:
- sin−1x=cos−11−x2−−−−−√=tan−1x1−x2√=cot−11−x2√x = sec−111−x2√=cosec−11x
- cos−1x=sin−11−x2−−−−−√=tan−11−x2√x=cot−1x1−x2√ = sec−11x=cosec−111−x2√
- tan−1x=sin−1x1+x2√=cos−111+x2√=sec−11+x2−−−−−√ = cosec−11+x2√x=cot−11x
- cot−1x=sin−111+x2√=cos−1x1+x2√=sec−11x= sec−11+x2√x=cosec−11+x2−−−−−√
- sec−1x=tan−1x2−1√1=cot−11x2−1√=sin−1x2−1√x = cos−11x=cosec−1xx2−1√
- cosec−1x=sin−11x=tan−11x2−1√=cot−1x2−1−−−−−√=sec−1xx2−1√=cos−1x2−1√x
Some other properties of Inverse Trigonometric Function:
- tan−1xa2−x2√=sin−1xa
- cot−1xa2−x2√=cos−1xa
- tan−1ax2−a2√=cosec−1xa
- cot−1ax2−a2√=sec−1xa
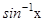 should not be confused with
should not be confused with 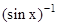 . In fact
. In fact 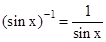 And similarly for other trigonometric functions.
And similarly for other trigonometric functions.