Relations and Functions - Test Papers

 CBSE Test Paper 01

Chapter 1 Relations and Functions

---

1. In Z , the set of integers, inverse of – 7 , w.r.t. ‘ * ‘ defined by a * b = a + b + 7 for all a,b∈Z$a,b\in Z$ ,is 
   1. -7
   2. -14
   3. 14
   4. 7
2. If A = { 1, 2, 3}, then the relation R = {(1, 2), (2, 3), (1, 3)} in A is ___. 
   1. transitive only
   2. reflexive only
   3. symmetric only
   4. symmetric and transitive only
3. A relation R on a set A is called an empty relation if 
   1. no element of A is related to any element of A
   2. every element of A is related to one element of A
   3. one element of A is related to all the elements of A
   4. every element of A is related to any element of A
4. Let f and g be two functions from R to R defined as f(x)={0,xisrational1,xisirrational}$f(x)=\left\{\begin{array}{c}0,xisrational\\ 1,xisirrational\end{array}\right\}$, g(x)={−1,xisrational0,xisirrational}$g(x)=\left\{\begin{array}{c}-1,xisrational\\ 0,xisirrational\end{array}\right\}$ then, (gof)(e) + (fog) (π)$(\pi )$ =. 
   1. 1
   2. 2
   3. -1
   4. 0
5. Let R be the relation on N defined as xRy if x + 2 y = 8. The domain of R is  
   1. {2, 4, 6, 8}
   2. {2, 4, 8}
   3. {1, 2, 3, 4}
   4. {2, 4, 6}
6. If n(A) = p and n(B) = q, then the number of relations from set A to set B = ________. 

7. A function is called an onto function, if its range is equal to ________. 

8. A binary operation * on a set X is said to be ________, if a * b = b * a, where a, b ∈$\in$ X. 

9. Find gof f(x) = |x|, g(x) = |5x + 1|. 

10. Show that function f: N →$\to$ N, given by f(x) = 2x, is one – one. 

11. Let S = {1, 2, 3} Determine whether the function f: S →$\to$ S defined as below have inverse.
    f = {(1, 1), (2, 2), (3, 3)}

12. Let f : {1, 3, 4} →$\to$ {1, 2, 5} and g : {1, 2, 5} →$\to$ {1, 3} be given by f = {(1, 2), (3, 5), (4, 1)} and g = {(1, 3), (2, 3), (5, 1)}. Write down gof.

13. Consider f: {1, 2, 3} →$\to$ {a, b, c} given by f(1) = a, f(2) = b and f(3) = c find f-1 and show that (f-1)-1 = f. 

14. Is g = {(1, 1), (2, 3), (3, 5), (4, 7)} a function? If g is described by g(x) = ax + b, then what value should be assigned to a and b. 

15. Show that the relation R defined by (a, b) R (c, d) ⇒$\Rightarrow$ a + d = b + c on the set N×$\times$N is an equivalence relation. 

16. Let the function f : R →$\to$ R be defined by f(x) = cosx, ∀$\mathrm{\forall }$x ∈$\in$ R. Show that f is neither one-one nor onto. 

17. Let L be the set of all lines in plane and R be the relation in L define if R = {(l1, L2 ): L1 is⊥$\mathrm{\perp }$ to L2 } .Show that R is symmetric but neither reflexive nor transitive. 

18. If the function f : R →$\to$ R is given by f (x) = x2 + 2 and g: R →$\to$ R is given by g(x)=xx−1;x≠1$g(x)=\frac{x}{x-1};x\ne 1$ then find fog and gof and hence find fog(2) and gof(- 3). 

CBSE Test Paper 01
Chapter 1 Relations and Functions

---

Solution

1. 1. -7
      Explanation: If ‘ e ‘ is the identity ,then a*e = a ⇒$\Rightarrow$a + e + 7 = a ⇒$\Rightarrow$ e = - 7 . Also,inverse of e is e itself. Hence , inverse of -7 is -7.
2. 1. transitive only
      Explanation: A relation R on a non-empty set A is said to be transitive if xRy and y Rz ⇒$\Rightarrow$ xRz, for all x ∈$\in$ R. Here, (1, 2) and (2, 3) belongs to R implies that (1, 3) belongs to R.
3. 1. no element of A is related to any element of A
      Explanation: For any set A ,an empty relation may be defined on A as: there is no element exists in the relation set which satisfies the relation for a given set A i.e.
      let A={1,2,3,4,5} and R={(a,b): a,b ∈$\in$ A and a+b= 10},so we get R={ } which is an empty relation.
4. 3. -1
      Explanation: (gof)(e) + (fog)(π$\pi$) =g(f(e)) + f(g(π$\pi$) = g(1) + f(0) = - 1 + 0 = -1.
5. 4. {2, 4, 6}
      Explanation: As xRy if x + 2 y = 8 , therefore, domain of the relation R is given by x = 8 – 2y ∈ N. When y = 1, ⇒$\Rightarrow$ x = 6, when y = 2, ⇒$\Rightarrow$ x =4 , when y =3 , ⇒$\Rightarrow$ x = 2. Therefore, domain is { 2, 4, 6 }.

6. 2pq

7. codomain

8. commutative

9. gof (x) = g [f(x)]
   = g [|x|]
   =| 5 |x| + 1 |

10. For, f(x1) = f(x2)
    2x1 = 2x2
    x1 = x2
    So, The function f is one – one

11. Since different elements have different images. So, f is one - one. Also, every element of codomain has pre-image so, f is onto
    Now f is one – one and onto, so that f is invertible with inverse f-1 = {(1, 1) (2, 2) (3, 3)}
12. f = {(1, 2), (3, 5), (4, 1)} and g = {(1, 3), (2, 3), (5, 1)}
    Now, f(1) = 2, f(3) = 5, f(4) = 1 and g(1) = 3, g(2) = 3, g(5) =1
    gof(x)=g(f(x))
    gof(1)=g(f(1))=g(2)=3
    g[f(3)] = g(5) = 1 and g[f(4)] = g(1) = 3
    Hence, gof = {(1, 3), (3, 1), (4, 3)}
13. f = {(1, a) (2, b) (3, c)}
    f-1 = { (a, 1) (b, 2) (c, 3)}
    (f -1) -1 = {(1, a) (2, b) (3, c)}
    Hence (f-1)-1 = f.
14. Yes, g is a function since every element in domain has a unique image in range.
    Now, Let g(x) = ax + b Then Given,
    g(1) = a + b = 1 &
    g(2) = 2a +b = 3
    Subtracting g(1) from g(2) Gives
    (2a + b) - (a + b) = a = 2 & Substituting It into g(1)
    We have b = -1
15. we have,a + b = b + a for all (a, b) ∈N×N$\in N\times N$, which implies (a,b) R (a,b).Thus, R is reflexive.
    Let (a,b),(c,d) ∈N×N$\in N\times N$ be such that
    (a, b) R (c, d)
    ⇒$\Rightarrow$ a + d= b + c
    ⇒$\Rightarrow$ d + a = c + b
    ⇒$\Rightarrow$ c + b = d + a
    ⇒$\Rightarrow$ (c, d) R (a, b) for all (a, b), (c, d) ∈N×N$\in N\times N$
    Hence R is symmetric.
    Let (a,b),(c,d),(e,f) ∈N×N$\in N\times N$ such that (a,b) R (c,d) and
    (c,d) R (e,f).Then,
    (a, b) R (c, d) ⇒$\Rightarrow$ a + d = b + c....... (1)
    (c, d) R (e, f) ⇒$\Rightarrow$ c + f = d + e .........(2)
    Adding (1) and (2)
    (a + d) + (c+f) = (b + c) + (d + e)
    a + f = b+ e
    (a, b) R (e, f)
    Hence, R is transitive
    So, R is an equivalence relation.

16. Given function, f(x) = cosx, ∀$\mathrm{\forall }$x ∈$\in$ R
    Now, f(π2)=cosπ2=0$f\left(\frac{\pi }{2}\right)=\cos \frac{\pi }{2}=0$
    ⇒f(−π2)=cosπ2=0$\Rightarrow f\left(\frac{-\pi }{2}\right)=\cos \frac{\pi }{2}=0$
    ⇒f(π2)=f(−π2)$\Rightarrow f\left(\frac{\pi }{2}\right)=f\left(\frac{-\pi }{2}\right)$
    But π2≠−π2=0$\frac{\pi }{2}\ne \frac{-\pi }{2}=0$
    So, f (x) is not one-one
    Now, f(x) = cosx, ∀$\mathrm{\forall }$x ∈$\in$ R is not onto as there is no pre-image for any real number. Which does not belong to the intervals [-1, 1], the range of cos x.

17. R is not reflexive, as a line L1 cannot be ⊥$\mathrm{\perp }$ to itself i.e (L1, L1 )∉$\notin$ R
    
    Now ( L1, L2)∈$\in$R
    ⇒$\Rightarrow$L1 ⊥$\mathrm{\perp }$ L2
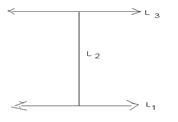
    ⇒$\Rightarrow$L2 ⊥$\mathrm{\perp }$ L1
    ⇒$\Rightarrow$(L2, L1)∈$\in$R
    R is symmetric
    Now (L1, L2) and (L2, L3) ∈$\in$ R
    i.e L1 ⊥$\mathrm{\perp }$ L2 and L2 ⊥$\mathrm{\perp }$ L3
    Then L1 can never be ⊥$\mathrm{\perp }$ to L3 in fact L1 || L3
    i.e (L1, L2) ∈$\in$ R, (L2, L3) ∈$\in$ R.
    But (L1, L3) ∉$\notin$ R
    R is not transitive.

18. We are given that, f : R →$\to$ R and g : R →$\to$ R defined as f(x) = x2 + 2 and g(x) = xx−1;x≠1$\frac{x}{x-1};x\ne 1$.
    First we see whether fog and gof exist for the given functions.
    Since, range f ⊆$\subseteq$ domain g and range g ⊆$\subseteq$ domain f
    Hence,fog and gof exist for the given functions.
    Now, for any x ∈$\in$ R - {1}, we have (fog)(x) = f[g(x)]
    = f[xx−1]=(xx−1)2+2$f\left[\frac{x}{x-1}\right]={\left(\frac{x}{x-1}\right)}^2+2$
    =x2+2(x−1)2(x−1)2$=\frac{x^2+2(x-1{)}^2}{(x-1{)}^2}$= x2+2(x2+1−2x)(x−1)2$\frac{x^2+2\left(x^2+1-2x\right)}{(x-1{)}^2}$
    =3x2+2−4x(x−1)2$\frac{3x^2+2-4x}{(x-1{)}^2}$
    ∴$\therefore$ fog: R →$\to$ R is defined by
    (fog)(x)= 3x2−4x+2(x−1)2,x≠1$\frac{3x^2-4x+2}{(x-1{)}^2},x\ne 1$ ......(i)
    For any x ∈$\in$ R we have
    gof(x) = g[f(x)]
    = g(x2 + 2) = x2+2(x2+2)−1=x2+2x2+1$\frac{x^2+2}{\left(x^2+2\right)-1}=\frac{x^2+2}{x^2+1}$
    ∴$\therefore$ gof: R →$\to$ R is defined by
    (gof)(x) = x2+2x2+1$\frac{x^2+2}{x^2+1}$ ........(ii)
    On putting x = 2 in Eq. (i), we get
    fog(2) = 3×(2)2−4(2)+2(2−1)2$\frac{3\times (2{)}^2-4(2)+2}{(2-1{)}^2}$= 3×4−8+2(1)2$\frac{3\times 4-8+2}{(1{)}^2}$
    = 12 - 8 + 2 = 6
    On putting x = - 3 in Eq. (ii), we get
    gof(-3) = (−3)2+2(−3)2+1=9+29+1=1110