Three Dimensional Geometry - Test Papers

 CBSE Test Paper 01

Chapter 11 Three Dimensional Geometry

---

1. Write the vector equation of a line that passes through the given point whose position vector is a⃗ $\overrightarrow{a}$ and parallel to a given vector b⃗ $\overrightarrow{b}$ .

   1. r⃗ =a⃗ −λb⃗ $\overrightarrow{r}=\overrightarrow{a}-\lambda \overrightarrow{b}$,λ∈R$\lambda \in R$
   2. r⃗ =a⃗ +λb⃗ $\overrightarrow{r}=\overrightarrow{a}+\lambda \overrightarrow{b}$, λ∈R$\lambda \in R$
   3. r⃗ =−a⃗ +λb⃗ $\overrightarrow{r}=-\overrightarrow{a}+\lambda \overrightarrow{b}$,λ∈R$\lambda \in R$
   4. r⃗ =−a⃗ −λb⃗ $\overrightarrow{r}=-\overrightarrow{a}-\lambda \overrightarrow{b}$, λ∈R$\lambda \in R$

2. If a line has the direction ratios – 18, 12, – 4, then what are its direction cosines ?

   1. 911,611,−211$\frac{9}{11},\frac{6}{11},\frac{-2}{11}$
   2. −911,611,−211$\frac{-9}{11},\frac{6}{11},\frac{-2}{11}$
   3. −911,611,211$\frac{-9}{11},\frac{6}{11},\frac{2}{11}$
   4. −711,611,−311$\frac{-7}{11},\frac{6}{11},\frac{-3}{11}$

3. In the Cartesian form two lines x−x1a1=y−y1b1=z−z1c1$\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1}$and x−x2a2=y−y2b2=z−z2c2$\frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2}$are coplanar if 

   1. ∣∣∣∣x2−x1a1−a2y2−y1b1b2z2−z1c1c2∣∣∣∣=0$\left|\begin{array}{ccc}{x}_2-x_1& y_2-y_1& z_2-z_1\\ a_1& b_1& c_1\\ -a_2& b_2& c_2\end{array}\right|=0$
   2. ∣∣∣∣x2−x1a1a2y2−y1b1b2z2−z1c1−c2∣∣∣∣=0$\left|\begin{array}{ccc}{x}_2-x_1& y_2-y_1& z_2-z_1\\ a_1& b_1& c_1\\ a_2& b_2& -c_2\end{array}\right|=0$
   3. ∣∣∣∣x2−x1a1a2y2−y1b1b2z2−z1c1c2∣∣∣∣=0$\left|\begin{array}{ccc}{x}_2-x_1& y_2-y_1& z_2-z_1\\ a_1& b_1& c_1\\ a_2& b_2& c_2\end{array}\right|=0$
   4. ∣∣∣∣x2−x1a1a2y2−y1b1−b2z2−z1c1c2∣∣∣∣=0$\left|\begin{array}{ccc}{x}_2-x_1& y_2-y_1& z_2-z_1\\ a_1& b_1& c_1\\ a_2& -b_2& c_2\end{array}\right|=0$

4. Express the Cartesian equation of a line that passes through two points(x1, y1, z1)$\left(x_1,y_1,z_1\right)$ and (x2, y2, z2)$\left(x_2,y_2,z_2\right)$ . 

   1. x+x1x2−x1=y−y1y2+y1=z−z1z2−z1$\frac{x+x_1}{x_2-x_1}=\frac{y-y_1}{y_2+y_1}=\frac{z-z_1}{z_2-z_1}$
   2. x−x1x2−x1=y−y1y2−y1=z+z1z2−z1$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z+z_1}{z_2-z_1}$
   3. x−x1x2−x1=y−y1y2+y1=z−z1z2−z1$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2+y_1}=\frac{z-z_1}{z_2-z_1}$
   4. x−x1x2−x1=y−y1y2−y1=z−z1z2−z1$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$

5. Two lines r⃗ =a1→+λb1→andr⃗ =a2→+μb2→$\overrightarrow{r}=\overrightarrow{a_1}+\lambda \overrightarrow{b_1}and\overrightarrow{r}=\overrightarrow{a_2}+\mu \overrightarrow{b_2}$ are coplanar if 

   1. (a2→−a1→).(−b1→×−b2−→−)=0$\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right).\left(-\overrightarrow{b_1}\times \overrightarrow{-b_2}\right)=0$
   2. (a2→−a1→).(b1→×b2→)=0$\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right).\left(\overrightarrow{b_1}\times \overrightarrow{b_2}\right)=0$
   3. (a2→−a1→).(−b1→×b2→)=0$\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right).\left(-\overrightarrow{b_1}\times \overrightarrow{b_2}\right)=0$
   4. (a2→−a1→).(b1→×−b2→)=0$\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right).\left(\overrightarrow{b_1}\times -\overrightarrow{b_2}\right)=0$
6. Direction ratios of two _________ lines are proportional.
7. If l, m, n are the direction cosines of a line, then l2 + m2 + n2 = ________.
8. The distance of a point P(a, b, c) from x-axis is ________.

9. Find the vector equation for the line passing through the points (-1,0,2) and (3,4,6). 

10. Write the vector equation of the plane passing through the point (a, b, c) and parallel to the plane r⃗ ⋅(i^+j^+k^)=2.$\overrightarrow{r}\cdot (\hat{i}+\hat{j}+\hat{k})=2.$ 

11. Write the equation of a plane which is at a distance of 53–√$5\sqrt{3}$ units from origin and the normal to which is equally inclined to coordinate axes. 

12. Find angle between lines x2=y2=z1,x−54=y−21=z−38$\frac{x}{2}=\frac{y}{2}=\frac{z}{1},\frac{x-5}{4}=\frac{y-2}{1}=\frac{z-3}{8}$. 

13. The x - coordinate of a point on the line joining the points Q(2, 2, 1) and R(5, 1, -2) is 4. Find its z - coordinate. 

14. Find the vector and Cartesian equation of the line through the point (5, 2,-4) and which is parallel to the vector 3i^+2j^−8k^$3\hat{i}+2\hat{j}-8\hat{k}$. 

15. Write the vector equations of following lines and hence find the distance between them.
    x−12=y−23=z+46,$\frac{x-1}{2}=\frac{y-2}{3}=\frac{z+4}{6},$ x−34=y−36=z+512$\frac{x-3}{4}=\frac{y-3}{6}=\frac{z+5}{12}$

16. The points A(4, 5,10), B(2, 3,4) and C(1, 2, -1) are three vertices of parallelogram ABCD. Find the vector equations of sides A and BC and also find coordinates of point D. 

17. Find the shortest distance between the lines whose vector equations are
    r→=(1−t)i^+(t−2)j^+(3−2t)k^$\overrightarrow{r}=(1-t)\hat{i}+(t-2)\hat{j}+(3-2t)\hat{k}$
    r→=(s+1)i^+(2s−1)j^−(2s+1)k^$\overrightarrow{r}=(s+1)\hat{i}+(2s-1)\hat{j}-(2s+1)\hat{k}$

18. Find the distance of the point (-1, -5, -10) from the point of intersection of the line r⃗ =(2i^−j^+2k^)+λ(3i^+4j^+2k^)$\overrightarrow{r}=\left(2\hat{i}-\hat{j}+2\hat{k}\right)+\lambda \left(3\hat{i}+4\hat{j}+2\hat{k}\right)$and the plane r⃗ .(i^−j^+k^)=5$\overrightarrow{r}.\left(\hat{i}-\hat{j}+\hat{k}\right)=5$. 

CBSE Test Paper 01
Chapter 11 Three Dimensional Geometry

---

Solution

1. 2. r⃗ =a⃗ +λb⃗ $\overrightarrow{r}=\overrightarrow{a}+\lambda \overrightarrow{b}$, λ∈R$\lambda \in R$
      Explanation: The vector equation of a line that passes through the given point whose position vector isa⃗ $\overrightarrow{a}$ and parallel to a given vector b⃗ $\overrightarrow{b}$ is given by : r⃗ =a⃗ +λb⃗ $\overrightarrow{r}=\overrightarrow{a}+\lambda \overrightarrow{b}$
      λ∈R$\lambda \in R$
      Where, r→=xi^+yj^+zk^$\overrightarrow{r}=x\hat{i}+y\hat{j}+z\hat{k}$
      a→=a1i^+b1j^+c1k^$\overrightarrow{a}=a_1\hat{i}+b_1\hat{j}+c_1\hat{k}$
      b→=a1i^+b1j^+c1k^$\overrightarrow{b}=a_1\hat{i}+b_1\hat{j}+c_1\hat{k}$
2. 2. −911,611,−211$\frac{-9}{11},\frac{6}{11},\frac{-2}{11}$
      Explanation: If a line has the direction ratios -18, 12, -4, then its direction cosines are given by:
      l=−18(−18)2+(12)2+(−4)2√$l=\frac{-18}{\sqrt{{(-18)}^2+{(12)}^2+{(-4)}^2}}$
      −18324+144+16√=−18484√$\frac{-18}{\sqrt{324+144+16}}=\frac{-18}{\sqrt{484}}$
      =−1822=−911$=\frac{-18}{22}=\frac{-9}{11}$
      m=12(−18)2+(12)2+(−4)2√$m=\frac{12}{\sqrt{{(-18)}^2+{(12)}^2+{(-4)}^2}}$
      =12324+144+16√=12484√$=\frac{12}{\sqrt{324+144+16}}=\frac{12}{\sqrt{484}}$
      =1222=611$=\frac{12}{22}=\frac{6}{11}$
      n=−4(−18)2+(12)2+(−4)2√$n=\frac{-4}{\sqrt{{(-18)}^2+{(12)}^2+{(-4)}^2}}$
      =−4324+144+16√=−4484√$=\frac{-4}{\sqrt{324+144+16}}=\frac{-4}{\sqrt{484}}$
      =−422=−211$=\frac{-4}{22}=\frac{-2}{11}$
3. 3. ∣∣∣∣x2−x1a1a2y2−y1b1b2z2−z1c1c2∣∣∣∣=0$\left|\begin{array}{ccc}{x}_2-x_1& y_2-y_1& z_2-z_1\\ a_1& b_1& c_1\\ a_2& b_2& c_2\end{array}\right|=0$.
      Explanation: In the Cartesian form two lines
      x−x1a1=y−y1b1=z−z1c1$\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1}$
      and
      x−x2a2=y−y2b2=z−z2c2$\frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2}$
      are coplanar if
      ∣∣∣∣x2−x1a1a2y2−y1b1b2z2−z1c1c2∣∣∣∣=0$\left|\begin{array}{ccc}{x}_2-x_1& y_2-y_1& z_2-z_1\\ a_1& b_1& c_1\\ a_2& b_2& c_2\end{array}\right|=0$
4. 4. x−x1x2−x1=y−y1y2−y1=z−z1z2−z1$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$
      Explanation: The Cartesian equation of a line that passes through two points (x1, y1, z1)$\left(x_1,y_1,z_1\right)$ and (x2, y2, z2)$\left(x_2,y_2,z_2\right)$ is given by : x−x1x2−x1=y−y1y2−y1=z−z1z2−z1$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$
5. 2. (a2→−a1→).(b1→×b2→)=0$\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right).\left(\overrightarrow{b_1}\times \overrightarrow{b_2}\right)=0$
      Explanation: In vector form: Two lines r⃗ =a1→+λb1→andr⃗ =a2→+μb2→$\overrightarrow{r}=\overrightarrow{a_1}+\lambda \overrightarrow{b_1}and\overrightarrow{r}=\overrightarrow{a_2}+\mu \overrightarrow{b_2}$are coplanar if
6. Parallel
7. 1
8. b2+c2−−−−−−√$\sqrt{b^2+c^2}$

9. Let a→$\overrightarrow{a}$ and b→$\overrightarrow{b}$ be the p.v of the points A (-1,0,2) and B (3, 4, 6)
   r⃗ =a⃗ +λ(b⃗ −a⃗ )$\overrightarrow{r}=\overrightarrow{a}+\lambda \left(\overrightarrow{b}-\overrightarrow{a}\right)$
   =(−i^+2k^)+λ(4i^+4j^+4k^)$=\left(-\hat{i}+2\hat{k}\right)+\lambda \left(4\hat{i}+4\hat{j}+4\hat{k}\right)$

10. According to the question, The required plane is passing through the point (a,b,c)$(a,b,c)$ whose position vector is p⃗ =ai^+bj^+ck^$\overrightarrow{p}=a\hat{i}+b\hat{j}+c\hat{k}$ and is parallel to the plane r⃗ ⋅(i^+j^+k^)=2$\overrightarrow{r}\cdot (\hat{i}+\hat{j}+\hat{k})=2$
    ∴$\therefore$ it is normal to the vector
    n⃗ =i^+j^+k^$\overrightarrow{n}=\hat{i}+\hat{j}+\hat{k}$
    Required equation of plane is
    (r⃗ −p⃗ ).n⃗ =0⇒r⃗ .n⃗ =p⃗ .n⃗ $(\overrightarrow{r}-\overrightarrow{p}).\overrightarrow{n}=0\Rightarrow \overrightarrow{r}.\overrightarrow{n}=\overrightarrow{p}.\overrightarrow{n}$
    ⇒$\Rightarrow$ r⃗ .(i^+j^+k^)=(ai^+b^+ck^)⋅(i^+ȷ^+k^)$\overrightarrow{r}.(\hat{i}+\hat{j}+\hat{k})=(a\hat{i}+\hat{b}+c\hat{k})\cdot (\hat{i}+\hat{ȷ}+\hat{k})$
    ∴r⃗ .(i^+j^+k^)=a+b+c$\therefore \overrightarrow{r}.(\hat{i}+\hat{j}+\hat{k})=a+b+c$

11. According to the question, the normal to the plane is equally inclined with coordinates axes, and the distance of the plane from origin is 53–√$5\sqrt{3}$ units
    ∴$\therefore$ the direction cosines are 13√,13√ and 13√$\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}\text{ and }\frac{1}{\sqrt{3}}$
    The required equation of plane is
    13√⋅x+13√⋅y+13√⋅z=53–√$\frac{1}{\sqrt{3}}\cdot x+\frac{1}{\sqrt{3}}\cdot y+\frac{1}{\sqrt{3}}\cdot z=5\sqrt{3}$
    ⇒x+y+z=5×3$\Rightarrow x+y+z=5\times 3$
    ⇒x+y+z=15$\Rightarrow x+y+z=15$
    [∵$\because$ If l, m and n are direction cosines of normal to the plane and P is a distance of a plane from origin, then the equation of plane is given by lx+my+nz=p$lx+my+nz=p$]

12. x−02=y−02=z−01$\frac{x-0}{2}=\frac{y-0}{2}=\frac{z-0}{1}$
    x−54=y−21=z−38$\frac{x-5}{4}=\frac{y-2}{1}=\frac{z-3}{8}$
    a1 = 2, b1 = 2, c1 = 1
    a2 = 4, b2 = 1, c2 = 8
    cosθ=∣∣b⃗ 1.b⃗ 2∣∣∣∣b⃗ 1∣∣∣∣b⃗ 2∣∣$\cos \theta =\frac{\left|{\overrightarrow{b}}_1.{\overrightarrow{b}}_2\right|}{\left|{\overrightarrow{b}}_1\right|\left|{\overrightarrow{b}}_2\right|}$
    =∣∣∣2(4)+2(1)+1(8)22+22+1√42+12+82√∣∣∣$=\left|\frac{2(4)+2(1)+1(8)}{\sqrt{2^2+2^2+1}\sqrt{4^2+1^2+8^2}}\right|$
    =∣∣8+2+89√81√∣∣$=\left|\frac{8+2+8}{\sqrt{9}\sqrt{81}}\right|$
    =1827$=\frac{18}{27}$
    =23$=\frac{2}{3}$
    θ=cos−1(23)$\theta ={\cos }^{-1}\left(\frac{2}{3}\right)$

13. Let the point P divide QR in the ratio λ:1$\lambda :1$, then the co-ordinate of P are
    (5λ+2λ+1,λ+2λ+1,−2λ+1λ+1)$\left(\frac{5\lambda +2}{\lambda +1},\frac{\lambda +2}{\lambda +1},\frac{-2\lambda +1}{\lambda +1}\right)$
    But x - coordinate of P is 4. Therefore,
    5λ+2λ+1=4⇒λ=2$\frac{5\lambda +2}{\lambda +1}=4\Rightarrow \lambda =2$
    Hence, the z - coordinate of P is −2λ+1λ+1=−1$\frac{-2\lambda +1}{\lambda +1}=-1$.

14. a⃗ =5i^+2j^−4k^,b⃗ =3i^+2j^−8k^$\overrightarrow{a}=5\hat{i}+2\hat{j}-4\hat{k},\overrightarrow{b}=3\hat{i}+2\hat{j}-8\hat{k}$
    Vector equation of line is
    r⃗ =a⃗ +λb⃗ $\overrightarrow{r}=\overrightarrow{a}+\lambda \overrightarrow{b}$
    =5i^+2j^−4k^+λ(3i^+2j^−8k^)$=5\hat{i}+2\hat{j}-4\hat{k}+\lambda (3\hat{i}+2\hat{j}-8\hat{k})$
    Cartesian equation is
    xi^+yj^+zk^=5i^+2j^−4k^+λ(3i^+2j^−8k^)$x\hat{i}+y\hat{j}+z\hat{k}=5\hat{i}+2\hat{j}-4\hat{k}+\lambda (3\hat{i}+2\hat{j}-8\hat{k})$
    ⇒xi^+yj^+zk^=(5+3λ)i^+(2+2λ)j^+(−4−8λ)k^$\Rightarrow x\hat{i}+y\hat{j}+z\hat{k}=(5+3\lambda )\hat{i}+(2+2\lambda )\hat{j}+(-4-8\lambda )\hat{k}$
    ⇒x=5+3λ,y=2+2λ,z=−4−8λ$\Rightarrow x=5+3\lambda ,y=2+2\lambda ,z=-4-8\lambda$
    ⇒x−53=y−22=z+4−8$\Rightarrow \frac{x-5}{3}=\frac{y-2}{2}=\frac{z+4}{-8}$=λ$=\lambda$
    Therefore, required equation is,
    x−53=y−22=z+4−8$\frac{x-5}{3}=\frac{y-2}{2}=\frac{z+4}{-8}$

15. The given equations of lines are
    x−12=y−23=z+46$\frac{x-1}{2}=\frac{y-2}{3}=\frac{z+4}{6}$
    and x−34=y−36=z+512$\frac{x-3}{4}=\frac{y-3}{6}=\frac{z+5}{12}$
    Now, the vector equation of given lines are
    r⃗ =(i^+2j^−4k^)+λ(2i^+3j^+6k^)$\overrightarrow{r}=(\hat{i}+2\hat{j}-4\hat{k})+\lambda (2\hat{i}+3\hat{j}+6\hat{k})$......(i)
    [∵$\because$ vector form of equation of line is r⃗ =a⃗ +λb⃗ ]$\overrightarrow{r}=\overrightarrow{a}+\lambda \overrightarrow{b}]$
    and r⃗ =(3i+3j^−5k^)+μ(4i^+6j^+12k^)$\overrightarrow{r}=(3i+3\hat{j}-5\hat{k})+\mu (4\hat{i}+6\hat{j}+12\hat{k})$...................(ii)
    Here, a1→=i^+2j^−4k^,b1→=2i^+3j^+6k^$\overrightarrow{a_1}=\hat{i}+2\hat{j}-4\hat{k},\overrightarrow{b_1}=2\hat{i}+3\hat{j}+6\hat{k}$
    and a2→=3i^+3j^−5k^,b2→=4i^+6j^+12k^$\overrightarrow{a_2}=3\hat{i}+3\hat{j}-5\hat{k},\overrightarrow{b_2}=4\hat{i}+6\hat{j}+12\hat{k}$
    Now, a2→−a1→=(3i^+3j^−5k^)−(i^+2j^−4k^)$\overrightarrow{a_2}-\overrightarrow{a_1}=(3\hat{i}+3\hat{j}-5\hat{k})-(\hat{i}+2\hat{j}-4\hat{k})$
    =2i^+j^−k^$=2\hat{i}+\hat{j}-\hat{k}$.................(iii)
    and b1→×b2→=∣∣∣∣∣i^24j^36k^612∣∣∣∣∣$\overrightarrow{b_1}\times \overrightarrow{b_2}=\left|\begin{array}{lll}\hat{i}& \hat{j}& \hat{k}\\ 2& 3& 6\\ 4& 6& 12\end{array}\right|$
    =i^(36−36)−j^(24−24)+k^(12−12)$=\hat{i}(36-36)-\hat{j}(24-24)+\hat{k}(12-12)$
    =0i^−0^j^+0k^=0⃗ $=0\hat{i}-\hat{0}\hat{j}+0\hat{k}=\overrightarrow{0}$
    ⇒b⃗ 1×b⃗ 2=0⃗ ,$\Rightarrow {\overrightarrow{b}}_1\times {\overrightarrow{b}}_2=\overrightarrow{0},$
    i.e. Vector b1 is parallel to b⃗ 2${\overrightarrow{b}}_2$
    [∵ if a⃗ ×b⃗ =0⃗ , then a⃗ ∥b⃗ ]$[\because \text{ if }\overrightarrow{a}\times \overrightarrow{b}=\overrightarrow{0},\text{ then }\overrightarrow{a}\Vert \overrightarrow{b}]$
    Thus, two lines are parallel.
    ∴b⃗ =(2i^+3j^+6k^)$\therefore \overrightarrow{b}=(2\hat{i}+3\hat{j}+6\hat{k})$...................(iv)
    [since, DR's of given lines are proportional]
    Since, the two lines are parallel, we use the formula for shortest distance between two parallel lines
    d=∣∣∣b⃗ ×(a⃗ 2−a1→)|b⃗ |∣∣∣$d=\left|\frac{\overrightarrow{b}\times \left({\overrightarrow{a}}_2-\overrightarrow{a_1}\right)}{|\overrightarrow{b}|}\right|$
    ⇒d=∣∣∣(2i^+3j^+6k^)×(2i^+j^−k^)(2)2+(3)2+(6)2√∣∣∣$\Rightarrow d=\left|\frac{(2\hat{i}+3\hat{j}+6\hat{k})\times (2\hat{i}+\hat{j}-\hat{k})}{\sqrt{(2{)}^2+(3{)}^2+(6{)}^2}}\right|$..............(v)
    [from Eqs. (iii) and (iv) ]
    Now, (2^i+3j^+6k^)×(2i^+j^−k^)$(\hat{2}i+3\hat{j}+6\hat{k})\times (2\hat{i}+\hat{j}-\hat{k})$
    =∣∣∣∣∣i^22j^31k^6−1∣∣∣∣∣$=\left|\begin{array}{ccc}\hat{i}& \hat{j}& \hat{k}\\ 2& 3& 6\\ 2& 1& -1\end{array}\right|$
    =i^(−3−6)−j^(−2−12)+k^(2−6)$=\hat{i}(-3-6)-\hat{j}(-2-12)+\hat{k}(2-6)$
    =−9i^+14j^−4k^$=-9\hat{i}+14\hat{j}-4\hat{k}$
    From Eq, (v), we get
    d=∣∣∣−9i^+14j^−4k^49√∣∣∣=(−9)2+(14)2+(−4)2√7$d=\left|\frac{-9\hat{i}+14\hat{j}-4\hat{k}}{\sqrt{49}}\right|=\frac{\sqrt{(-9{)}^2+(14{)}^2+(-4{)}^2}}{7}$
    ∴d=81+196+16√7=293√7$\therefore d=\frac{\sqrt{81+196+16}}{7}=\frac{\sqrt{293}}{7}$units

16. The vector equation of a side of a parallelogram, when two points are given, is r⃗ =a⃗ +λ(b⃗ −a⃗ ).$\overrightarrow{r}=\overrightarrow{a}+\lambda (\overrightarrow{b}-\overrightarrow{a}).$ Also, the diagonals of a parallelogram intersect each other at mid-point.
    Given points are A (4,5,10), B (2, 3,4) and C(1,2,-1).
    
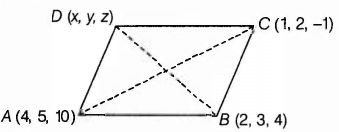
    We know that, two point vector form of line is
    given by
    r⃗ =a⃗ +λ(b⃗ −a⃗ )$\overrightarrow{r}=\overrightarrow{a}+\lambda (\overrightarrow{b}-\overrightarrow{a})$.......................... ......(i)
    where, a⃗ $\overrightarrow{a}$ and b⃗ $\overrightarrow{b}$ are the position vector of points through which the line is passing through. Here, for line AB, position vectors are
    a⃗ =OA→=4i^+5j^+10k^$\overrightarrow{a}=\overrightarrow{OA}=4\hat{i}+5\hat{j}+10\hat{k}$
    and b⃗ =OB→=2i^+3j^+4k^$\overrightarrow{b}=\overrightarrow{OB}=2\hat{i}+3\hat{j}+4\hat{k}$
    Using Equation. (i), the required equation of line AB is
    r⃗ =(4i^+5j^+10k^)+λ[(2i^+3j^+4k^)$\overrightarrow{r}=(4\hat{i}+5\hat{j}+10\hat{k})+\lambda [(2\hat{i}+3\hat{j}+4\hat{k})$−(4i^+5j^+10k^)]$-(4\hat{i}+5\hat{j}+10\hat{k})]$
    ⇒r⃗ =(4i^+5j^+10k^)+λ(−2i^−2j^−6k^)$\Rightarrow \overrightarrow{r}=(4\hat{i}+5\hat{j}+10\hat{k})+\lambda (-2\hat{i}-2\hat{j}-6\hat{k})$
    Similarly, vector equation of line BC, where B(2,3,4) and C (1, 2, -1) is
    r⃗ =(2i^+3j^+4k^)+μ(i^+2j^−k^)$\overrightarrow{r}=(2\hat{i}+3\hat{j}+4\hat{k})+\mu (\hat{i}+2\hat{j}-\hat{k})$−(2i^+3j^+4k^)]$-(2\hat{i}+3\hat{j}+4\hat{k})]$
    ⇒r⃗ =(2i^+3j^+4k^)+μ(−i^−j^−5k^)$\Rightarrow \overrightarrow{r}=(2\hat{i}+3\hat{j}+4\hat{k})+\mu (-\hat{i}-\hat{j}-5\hat{k})$
    We know that, mid-point of diagonal BD
    = Mid-point of diagonal AC
    [∴$\therefore$ diagonal of a parallelogram bisect each other]
    ∴(x+22,y+32,z+42)=(4+12,5+22,10−12)$\therefore \left(\frac{x+2}{2},\frac{y+3}{2},\frac{z+4}{2}\right)=\left(\frac{4+1}{2},\frac{5+2}{2},\frac{10-1}{2}\right)$
    Therefore, on comparing corresponding coordinates, we get
    x+22=52,y+32=72 and z+42=92$\frac{x+2}{2}=\frac{5}{2},\frac{y+3}{2}=\frac{7}{2}\text{ and }\frac{z+4}{2}=\frac{9}{2}$
    ⇒x=3,y=4 and z=5$\Rightarrow x=3,y=4\text{ and }z=5$
    Therefore, coordinates of point D (x, y, z) is (3,4,5) and vector equations of sides AB and BC are
    r⃗ =(4i^+5j^+10k^)−λ(2i^+2j^+6k^)$\overrightarrow{r}=(4\hat{i}+5\hat{j}+10\hat{k})-\lambda (2\hat{i}+2\hat{j}+6\hat{k})$ and
    r⃗ =(2i^+3j^+4k^)−μ(i^+j^+ 5k^),$\overrightarrow{r}=(2\hat{i}+3\hat{j}+4\hat{k})-\mu \widehat{(i}+\hat{j}+5\hat{k}),$ respectively.
    r⃗ =i^−2j^+3k^+t(−i^+j^−2k^)$\overrightarrow{r}=\hat{i}-2\hat{j}+3\hat{k}+t(-\hat{i}+\hat{j}-2\hat{k})$
    r⃗ =i^−j^−k^+s(i^+2j^−2k^)$\overrightarrow{r}=\hat{i}-\hat{j}-\hat{k}+s(\hat{i}+2\hat{j}-2\hat{k})$
    a1→=i^−2j^+3k^$\overrightarrow{a_1}=\hat{i}-2\hat{j}+3\hat{k}$
    b1→=−i^+j^−2k^$\overrightarrow{b_1}=-\hat{i}+\hat{j}-2\hat{k}$
    a⃗ 2=i^−j^−k^${\overrightarrow{a}}_2=\hat{i}-\hat{j}-\hat{k}$
    b⃗ 2=i^+2j^−2k^${\overrightarrow{b}}_2=\hat{i}+2\hat{j}-2\hat{k}$
    a⃗ 2−a1→=j^−4k^${\overrightarrow{a}}_2-\overrightarrow{a_1}=\hat{j}-4\hat{k}$
    b1→×b^2=∣∣∣∣∣i^−11j^12k^−2−2∣∣∣∣∣$\overrightarrow{b_1}\times {\hat{b}}_2=\left|\begin{array}{ccc}\hat{i}& \hat{j}& \hat{k}\\ -1& 1& -2\\ 1& 2& -2\end{array}\right|$

17. 2i^−4j^−3k^$2\hat{i}-4\hat{j}-3\hat{k}$
    (a⃗ 2−a⃗ 1)⋅(b⃗ 1×b⃗ 2)$\left({\overrightarrow{a}}_2-{\overrightarrow{a}}_1\right)\cdot \left({\overrightarrow{b}}_1\times {\overrightarrow{b}}_2\right)$=(0i⃗ +j⃗ −4k⃗ )⋅(2i⃗ −4j⃗ −3k⃗ )$=(0\overrightarrow{i}+\overrightarrow{j}-4\overrightarrow{k})\cdot (2\overrightarrow{i}-4\overrightarrow{j}-3\overrightarrow{k})$=0−4+12=8$=0-4+12=8$
    ∣∣b⃗ 1×b⃗ 2∣∣=(2)2+(−4)2+(−3)2−−−−−−−−−−−−−−−−−√$\left|{\overrightarrow{b}}_1\times {\overrightarrow{b}}_2\right|=\sqrt{(2{)}^2+(-4{)}^2+(-3{)}^2}$
    =29−−√$=\sqrt{29}$
    d=∣∣∣(a⃗ 2−a⃗ 1)(b⃗ 1×b⃗ 2)∣∣b⃗ 1×b⃗ 2∣∣∣∣∣=829√$d=\left|\frac{\left({\overrightarrow{a}}_2-{\overrightarrow{a}}_1\right)\left({\overrightarrow{b}}_1\times {\overrightarrow{b}}_2\right)}{\left|{\overrightarrow{b}}_1\times {\overrightarrow{b}}_2\right|}\right|=\frac{8}{\sqrt{29}}$

18. r⃗ =(2i^−j^+3k^)+λ(3i^+4j^+2k^)$\overrightarrow{r}=\left(2\hat{i}-\hat{j}+3\hat{k}\right)+\lambda \left(3\hat{i}+4\hat{j}+2\hat{k}\right)$
    ⇒x−23=y+14=z−22=λ$\Rightarrow \frac{x-2}{3}=\frac{y+1}{4}=\frac{z-2}{2}=\lambda$ ...(1)
    Any point on line (1) is,
    P(3λ+2,4λ−1,2λ+2)$P(3\lambda +2,4\lambda -1,2\lambda +2)$
    Now, r⃗ .(i^−j^+k^)=5$\overrightarrow{r}.\left(\hat{i}-\hat{j}+\hat{k}\right)=5$
    (xi^+yj^+zk^).(i^−j^+k^)=5$(x\hat{i}+y\hat{j}+z\hat{k}).(\hat{i}-\hat{j}+\hat{k})=5$
    x−y+z=5$x-y+z=5$ ...(2)
    Since point P lies on (2), therefore, from (2), we have,
    (3λ+2)−(4λ−1)+(2λ+2)=5$(3\lambda +2)-(4\lambda -1)+(2\lambda +2)=5$
    ⇒λ+5=5$\Rightarrow \lambda +5=5$
    ⇒λ=0$\Rightarrow \lambda =0$
    We get (2, -1, 2)
    as the coordinate of the point of intersection of the given line and the plane
    Now distance between the points (-1, -5, -10) and (2, -1, 2)
    req. distance =(2+1)2+(−1+5)2+(2+10)2−−−−−−−−−−−−−−−−−−−−−−−−−√$=\sqrt{{\left(2+1\right)}^2+{\left(-1+5\right)}^2+{\left(2+10\right)}^2}$
    = 9+16+144−−−−−−−−−−√$\sqrt{9+16+144}$=13