Three Dimensional Geometry - Exemplar Solutions
CBSE Class–12 Mathematics
NCERT Exemplar
Chapter - 11
Three Dimensional Geometry - Short Answer Questions
1. If the direction ratios of a line are 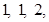 find the direction cosines of the line.
find the direction cosines of the line.
Sol. The direction cosines are given by
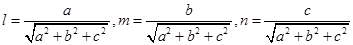
Here  are
are 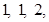 respectively.
respectively.
Therefore, 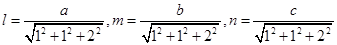
i.e., 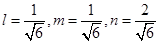 i.e.
i.e. 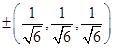 are D.C’s of the line.
are D.C’s of the line.
2 Find the direction cosines of the line passing through the points 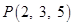 and
and 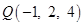 .
.
Sol. The direction cosines of a line passing through the points 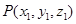 and
and 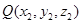 are
are
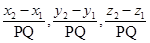 .
.
Here 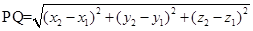
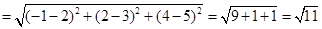
Here D.C.’s are
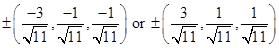 .
.
3. If a line makes an angle of ![]() with the positive direction of x, y, z-axes, respectively, then find its direction cosines.
with the positive direction of x, y, z-axes, respectively, then find its direction cosines.
Sol. The direction cosines of a line which makes an angle of 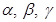 with the axes, are
with the axes, are 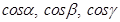
Therefore, D.C.’s of the line are 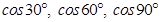 i.e.,
i.e., 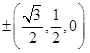
4. The 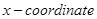 of a point on the line joining the points
of a point on the line joining the points 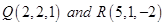 is 4. Find its
is 4. Find its 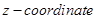 .
.
Sol. Let the point P divide QR in the ratio 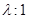 , then the co-ordinate of P are
, then the co-ordinate of P are
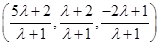
But 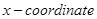 of P is 4. Therefore,
of P is 4. Therefore,
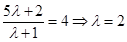
Hence, the 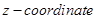 of P is
of P is 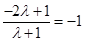 .
.
5. Find the distance of the point whose position vector is 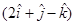 from the plane
from the plane 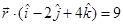
Sol. Let 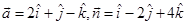 and d=9
and d=9
So, the required distance is 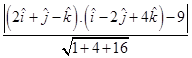
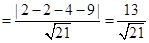 .
.
6. Find the distance of the point 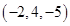 from the line
from the line 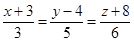
Sol. Let 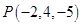 is the given point.
is the given point.
Any point 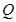 on the line is given by
on the line is given by 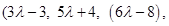
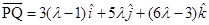 .
.
Since 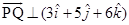 , we have
, we have
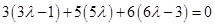
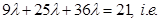
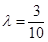
Thus 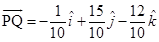
Hence 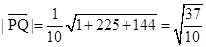 .
.
7. Find the coordinates of the point where the line through 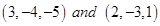 crosses the plane passing through three points
crosses the plane passing through three points 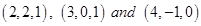 .
.
Sol. Equation of plane through three points 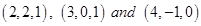 is
is
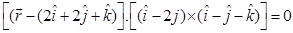
i.e., 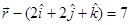 or
or 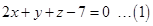
Equation of line through 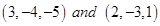 is
is
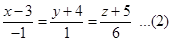
Any point on line (2) is 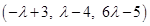 . This point lies on plane (1). Therefore,
. This point lies on plane (1). Therefore,
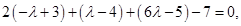 i.e.,
i.e., 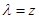
Hence the required point is 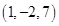 .
.
8. Find the distance of the point (–1, –5, – 10) from the point of intersection of the line 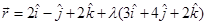 and the plane
and the plane 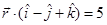 .
.
Sol. We have 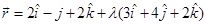 and
and 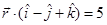
Solving these two equations, we get 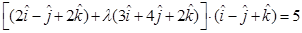 which gives
which gives 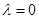 .
.
Therefore, the point of intersection of line and the plane is 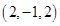 and the other given point is
and the other given point is 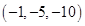 . Hence the distance between these two points is
. Hence the distance between these two points is
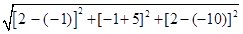 , i.e. 13
, i.e. 13
9. A plane meets the co-ordinate axes in 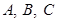 such that the centroid of the
such that the centroid of the 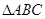 is the point
is the point 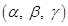 . Show that the equation of the plane is
. Show that the equation of the plane is 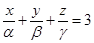
Sol. Let the equation of the plane be
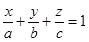
Then the co-ordinate of 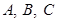 are
are 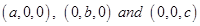 respectively. Centroid of the
respectively. Centroid of the 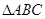 is
is
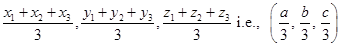
But co-ordinates of the centroid of the 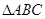 are
are 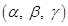 (given).
(given).
Therefore, 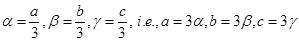
Thus, the equation of plane is
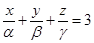
10 Find the angle between the lines whose direction cosines are given by the equations 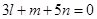 and
and 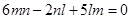 .
.
Sol. Eliminating 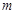 from the given two equations, we get
from the given two equations, we get
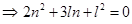
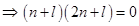
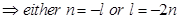
Now if 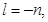 then
then 
and if 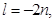 then
then 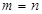 .
.
Thus, the direction ratios of two lines are proportional to 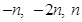 and
and 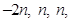
i.e. 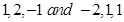 .
.
So, vectors parallel to these lines are
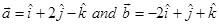 , respectively.
, respectively.
If 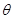 is the angle between the lines, then
is the angle between the lines, then
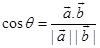
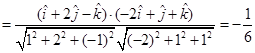
Hence, 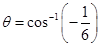 .
.
11. Find the co-ordinates of the foot of perpendicular drawn from the point 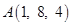 to the line joining the points
to the line joining the points 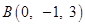 and
and 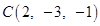 .
.
Sol. Let L be the foot of perpendicular drawn from the points 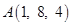 to the line passing through B and C as shown in the Fig. 11.2. The equation of line BC by using formula
to the line passing through B and C as shown in the Fig. 11.2. The equation of line BC by using formula 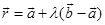 , the equation of the line BC is
, the equation of the line BC is
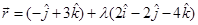
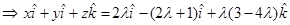
Comparing both sides, we get
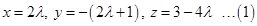
Thus, the co-ordinate of L are 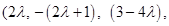
so, that the direction ratios of the line AL are 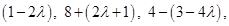 i.e.
i.e.
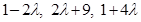
Since AL is perpendicular to BC, we have,
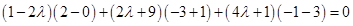
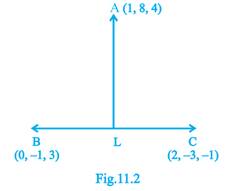
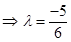
The required point is obtained by substituting the value of 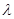 , in (1), which is
, in (1), which is 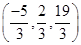 .
.
12. Find the image of the point 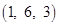 in the line
in the line 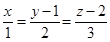 .
.
Sol. Let 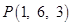 be the given point and let L be the foot of perpendicular from P to the given line.
be the given point and let L be the foot of perpendicular from P to the given line.
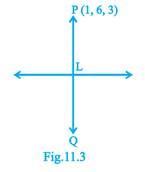
The coordinates of a general point on the given line are
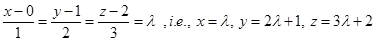
If the coordinates of L are 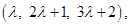 then the direction ratios of
then the direction ratios of 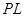 are
are 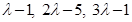 .
.
But the direction ratios of given line which is perpendicular to 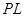 are
are 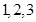 . Therefore,
. Therefore, 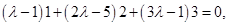 which gives
which gives 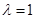 . Hence coordinates of
. Hence coordinates of 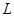 are
are 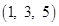 .
.
Let 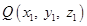 be the image of
be the image of 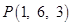 in the given line. Then
in the given line. Then 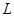 is the mid-point of
is the mid-point of 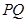 . Therefore,
. Therefore, 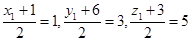
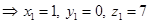
Hence, the image of 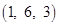 in the given line is
in the given line is 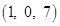 .
.
13. Find the image of the point having position vector 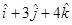 in the plane
in the plane 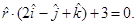
Sol. Let the given point be 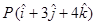 and
and 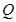 be the image of
be the image of 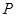 in the plane
in the plane 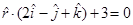 as shown in the Fig. 11.4.
as shown in the Fig. 11.4.
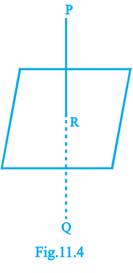
Then PQ is the normal to the plane. Since PQ passes through P and is normal to the given plane, so the equation of PQ is given by
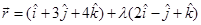
Since Q lies on the line PQ, the position vector of Q can be expressed as 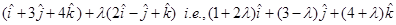
Since R is the mid point of PQ, the position vector of R is 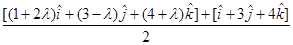
i.e., 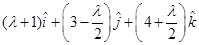
Again, since R lies on the plane 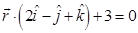 , we have
, we have
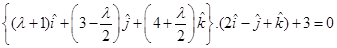
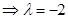
Hence, the position vector of Q is 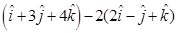 , i.e.,
, i.e.,  .
.
Choose the correct answer from the given four options in each of the Examples 14 to 19.
14.The coordinates of the foot of the perpendicular drawn from the point 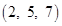 on the
on the 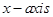 are given by
are given by
(A) 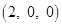
(B) 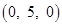
(C) 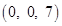
(D) 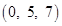
Sol. (A) is the correct Answer.
15. 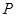 is a point on the line segment joining the points
is a point on the line segment joining the points 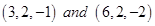 . If
. If 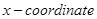 of
of 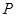 is 5, then its
is 5, then its 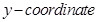 is
is
(A) 2
(B) 1
(C) –1
(D) –2
Sol. (A) is the correct answer. Let 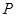 divides the line segment in the ratio of
divides the line segment in the ratio of 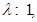
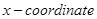 of the point
of the point 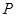 may be expressed as
may be expressed as 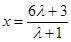 giving
giving 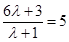 so that
so that 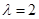 . Thus,
. Thus, 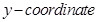 of
of 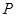 is
is 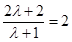 .
.
16. If α, β, γ are the angles that a line makes with the positive direction of x,yand z axes respectively, then the direction cosines of the line are.
(A) 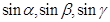
(B) 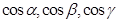
(C) 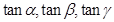
(D) 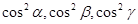
Sol. (B) is the correct answer.
17. The distance of a point 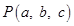 from
from 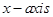 is
is
(A) 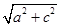
(B) 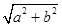
(C) 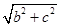
(D) 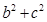
Sol. (C) is the correct answer. The required distance is the distance of 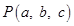 from
from 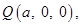 which is
which is 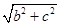 .
.
18. The equations of 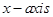 in space are
in space are
(A) 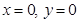
(B) 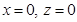
(C) 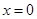
(D) 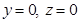
Sol. (D) is the correct answer. On 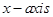 the
the 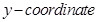 and
and 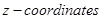 are zero.
are zero.
19. A line makes equal angles with co-ordinate axes. Direction cosines of this line are
(A) 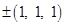
(B) 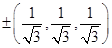
(C) 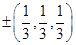
(D) 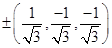
Sol. (B) is the correct answer. Let the line makes angle 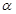 with each of the axis. Then, its direction cosines are
with each of the axis. Then, its direction cosines are 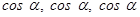 .
.
Since 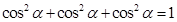 . Therefore,
. Therefore, 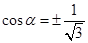
Fill in the blanks in each of the Examples from 20 to 22.
20. If a line makes angles 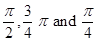 with
with 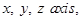 respectively, then its direction cosines are __________.
respectively, then its direction cosines are __________.
Sol. The direction cosines are 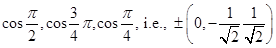
21. If a line makes angles 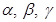 with the positive directions of the coordinate axes, then the value of
with the positive directions of the coordinate axes, then the value of 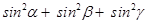 is __________.
is __________.
Sol. Note that

22. If a line makes an angle of 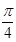 with each of y and z axes, then the angle which it makes with
with each of y and z axes, then the angle which it makes with 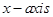 is __________.
is __________.
Sol. Let it makes angle 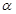 with
with 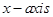 . Then
. Then 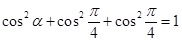 which after simplification gives
which after simplification gives 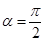 .
.
State whether the following statements are True or False in Examples 23 and 24.
23. The points 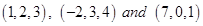 are collinear.
are collinear.
Sol. Let A, B, C be the points 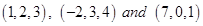 respectively. Then, the direction ratios of each of the lines AB and BC are proportional to
respectively. Then, the direction ratios of each of the lines AB and BC are proportional to 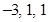 . Therefore, the statement is true.
. Therefore, the statement is true.
24. The vector equation of the line passing through the points 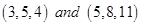 is
is 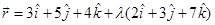
Sol. The position vector of the points 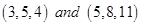 are
are
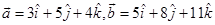 ,
,
and therefore, the required equation of the line is given by
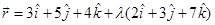 .
.
Hence, the statement is true.