Three Dimensional Geometry - Revision Notes
CBSE Class 12 Mathematics
Chapter-11
Three Dimensional Geometry
- Direction cosines of a line : Direction cosines of a line are the cosines of the angles made by the line with the positive direct ions of the coordinate axes.
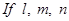 are the direct ion cosines of a line, then
are the direct ion cosines of a line, then 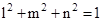
- Direct ion cosines of a line joining two points
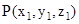 and
and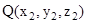 are
are 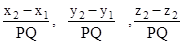
· where 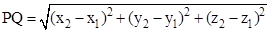
- Direction ratios of a line are the numbers which are proportional to the direct ion cosines of a line.
- If
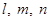 are the direct ion cosines and
are the direct ion cosines and 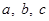 are the direct ion ratios of a line
are the direct ion ratios of a line
Then, 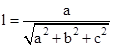 ,
,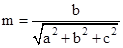 ,
,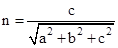
- Skew lines: Skew lines are lines in space which are neither parallel nor intersecting. They lie in different planes.
- Angle between two skew lines: Angle between skew lines is the angle between two intersecting lines drawn from any point (preferably through the origin) parallel to each of the skew lines.
- If
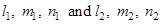 are the direction cosines of two lines; and
are the direction cosines of two lines; and 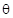 is the acute angle between the two lines; then,
is the acute angle between the two lines; then,
- Vector equation of a line that passes through the given point whose position vector is
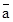 and parallel to a given vector
and parallel to a given vector 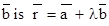
- Equation of a line through a point
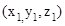 and having direct ion cosines
and having direct ion cosines 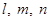 is
is 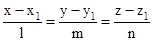
- The vector equation of a line which passes through two points whose position vectors are
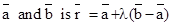
- Cartesian equation of a line that passes through two points
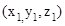 and
and 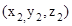 is
is 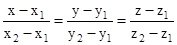
- If
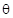 is the acute angle between
is the acute angle between 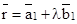 and
and 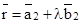 then,
then, - If
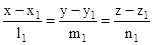 and
and 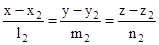 are the equations of two lines, then the acute angle between the two lines is given by
are the equations of two lines, then the acute angle between the two lines is given by 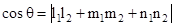
- Shortest distance between two skew lines is the line segment perpendicular to both the lines.
- Shortest distance between and is
- Shortest distance between the lines:
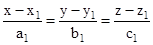 and
and 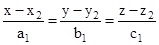 is
is
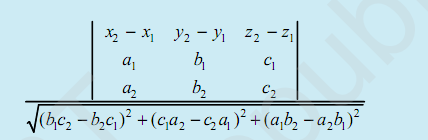
- Distance between parallel lines and is
- In the vector form, equation of a plane which is at a distance d from the origin, and is the unit vector normal to the plane through the origin is
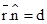
- Equation of a plane which is at a distance of d from the origin and the direction cosines of the normal to the plane as l, m, n is
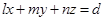 .
. - The equation of a plane through a point whose position vector is a and perpendicular to the vector is .
- Equation of a plane perpendicular to a given line with direction ratios A, B, C and passing through a given point
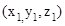 is
is 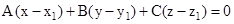
- Equation of a plane passing through three non collinear points
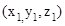 ,
, 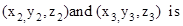
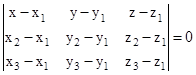
- Vector equation of a plane that contains three non collinear points having position vectors and is .
- Equation of a plane that cuts the coordinates axes at
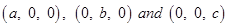 is
is 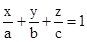 .
. - Vector equation of a plane that passes through the intersection of planes and is , where
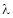 is any non-zero constant.
is any non-zero constant. - Cartesian equation of a plane that passes that passes through the intersection of two given planes
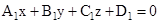 and
and 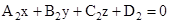 is
is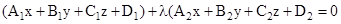
- Two lines and are coplanar if
- Two planes and are coplanar if
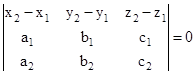
- In the vector form, if
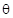 is the angle between the two planes, and , then
is the angle between the two planes, and , then - The angle
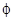 between the line and the plane is
between the line and the plane is - The angle
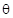 between the planes
between the planes 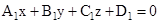 and
and 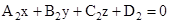 is given by
is given by 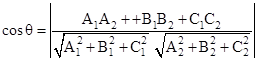
- The distance of a point whose position vector is from the plane is .
- The distance from a point
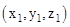 to the plane Ax + By + Cz + D = 0 is
to the plane Ax + By + Cz + D = 0 is 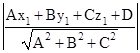
- Equation of any plane that is parallel to a plane that is parallel to a plane Ax + By + Cz + D = 0 is Ax + By + Cz + k = 0, where k is a different constant other than D.