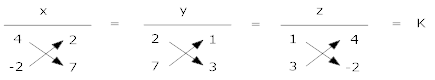Vector Algebra - Test Papers

CBSE Test Paper 01
Chapter 10 Vector Algebra

---

1. Find the angle between two vectors a⃗ $\overrightarrow{a}$ and b⃗ $\overrightarrow{b}$ with magnitudes 3–√$\sqrt{3}$ and 2, respectively, having a⃗ .b⃗ =6–√$\overrightarrow{a}.\overrightarrow{b}=\sqrt{6}$.

   1. π5$\frac{\pi }{5}$
   2. π3$\frac{\pi }{3}$
   3. π2$\frac{\pi }{2}$
   4. π4$\frac{\pi }{4}$

2. Find the angle between two vectors i^−2j^+3k^$\hat{i}-2\hat{j}+3\hat{k}$and 3i^−2j^+k^$3\hat{i}-2\hat{j}+\hat{k}$. 

   1. cos−1(47)${\cos }^{-1}\left(\frac{4}{7}\right)$
   2. cos−1(67)${\cos }^{-1}\left(\frac{6}{7}\right)$
   3. cos−1(59)${\cos }^{-1}\left(\frac{5}{9}\right)$
   4. cos−1(57)${\cos }^{-1}\left(\frac{5}{7}\right)$

3. Vector has 

   1. direction
   2. None of these
   3. magnitude
   4. magnitude as well as direction

4. Find the sum of the vectorsa⃗ =i^−2j^+k^,b⃗ =−2i^+4j^+5k^$\overrightarrow{a}=\hat{i}-2\hat{j}+\hat{k},\overrightarrow{b}=-2\hat{i}+4\hat{j}+5\hat{k}$ and c⃗ =i^−6j^−7k^$\overrightarrow{c}=\hat{i}-6\hat{j}-7\hat{k}$. 

   1. −i^+4j^−k^$-\hat{i}+4\hat{j}-\hat{k}$
   2. −4j^−k^$-4\hat{j}-\hat{k}$
   3. −i^−4j^−k^$-\hat{i}-4\hat{j}-\hat{k}$
   4. i^−4j^−k^$\hat{i}-4\hat{j}-\hat{k}$

5. Find the direction cosines of the vector i^+2j^+3k^$\hat{i}+2\hat{j}+3\hat{k}$. 

   1. 114√,214√,314√$\frac{1}{\sqrt{14}},\frac{2}{\sqrt{14}},\frac{3}{\sqrt{14}}$
   2. 114√,214√,−314√$\frac{1}{\sqrt{14}},\frac{2}{\sqrt{14}},-\frac{3}{\sqrt{14}}$
   3. 114√,−214√,314√$\frac{1}{\sqrt{14}},-\frac{2}{\sqrt{14}},\frac{3}{\sqrt{14}}$
   4. −114√,214√,314√$-\frac{1}{\sqrt{14}},\frac{2}{\sqrt{14}},\frac{3}{\sqrt{14}}$
6. The values of k which |ka⃗ |<|a⃗ |$|k\overrightarrow{a}|<|\overrightarrow{a}|$ and ka⃗ +12a⃗ $k\overrightarrow{a}+\frac{1}{2}\overrightarrow{a}$ is parallel to a⃗ $\overrightarrow{a}$ holds true are ________.
7. If r⃗ .a⃗ =0$\overrightarrow{r}.\overrightarrow{a}=0$, r⃗ .b⃗ =0$\overrightarrow{r}.\overrightarrow{b}=0$, and r⃗ .c⃗ =0$\overrightarrow{r}.\overrightarrow{c}=0$ for some non-zero vector r⃗ $\overrightarrow{r}$, then the value of a⃗ (b⃗ ×c⃗ )$\overrightarrow{a}(\overrightarrow{b}\times \overrightarrow{c})$ is ________.
8. The angle between two vectors a⃗ $\overrightarrow{a}$ and b⃗ $\overrightarrow{b}$ with magnitudes 3–√$\sqrt{3}$ and 4, respectively, a⃗ .b⃗ $\overrightarrow{a}.\overrightarrow{b}$ = 23–√$2\sqrt{3}$ is ________.

9. Find a⃗ ×b⃗ $\overrightarrow{a}\times \overrightarrow{b}$ if a⃗ =2i^+j^+3k^,b⃗ =3i^+5j^−2k^$\overrightarrow{a}=2\hat{i}+\hat{j}+3\hat{k},\overrightarrow{b}=3\hat{i}+5\hat{j}-2\hat{k}$. 

10. Find the projection of a⃗  on b⃗ ,$\overrightarrow{a}\text{ on }\overrightarrow{b},$ if a⃗ ⋅b⃗ =8$\overrightarrow{a}\cdot \overrightarrow{b}=8$ and b⃗ =2i^+6j^+3k^.$\overrightarrow{b}=2\hat{i}+6\hat{j}+3\hat{k}.$ 

11. a⃗ $\overrightarrow{a}$ Is unit vector and (x⃗ −a⃗ )(x⃗ +a⃗ )=8$\left(\overrightarrow{x}-\overrightarrow{a}\right)\left(\overrightarrow{x}+\overrightarrow{a}\right)=8$, Then find |x⃗ |$\left|\overrightarrow{x}\right|$. 

12. Find the position vector of the mid-point of the vector joining the points P (2, 3, 4) and Q(4,1, - 2) 

13. Find sine of the angle between the vectors. a⃗ =2i^−j^+3k^,b⃗ =i^+3j^+2k^$\overrightarrow{a}=2\hat{i}-\hat{j}+3\hat{k},\overrightarrow{b}=\hat{i}+3\hat{j}+2\hat{k}$. 

14. Find the projection of the vector i^+3j^+7k^$\hat{i}+3\hat{j}+7\hat{k}$ on the vector 7i^−j^+8k^$7\hat{i}-\hat{j}+8\hat{k}$ 

15. Let a⃗ =i^+j^+k^,b⃗ =4i^−2j^+3k^$\overrightarrow{a}=\hat{i}+\hat{j}+\hat{k},\overrightarrow{b}=4\hat{i}-2\hat{j}+3\hat{k}$ and c⃗ =i^−2j^+k^.$\overrightarrow{c}=\hat{i}-2\hat{j}+\hat{k}.$Find a vector of magnitude 6 units, which is parallel to the vector 2a⃗ −b⃗ +3c⃗ .$2\overrightarrow{a}-\overrightarrow{b}+3\overrightarrow{c}.$

16. Let a⃗ =i^+4j^+2k^,b⃗ =3i^−2j^+7k^$\overrightarrow{a}=\hat{i}+4\hat{j}+2\hat{k},\overrightarrow{b}=3\hat{i}-2\hat{j}+7\hat{k}$ and c⃗ =2i^−j^+4k^$\overrightarrow{c}=2\hat{i}-\hat{j}+4\hat{k}$ .Find a vector d⃗ $\overrightarrow{d}$ which is perpendicular to both a⃗ $\overrightarrow{a}$ and b⃗ $\overrightarrow{b}$ and c⃗ .d⃗ =15$\overrightarrow{c}.\overrightarrow{d}=15$. 

17. A girl walks 4 km towards west, then she walks 3 km in a direction 300${30}^0$ east of north and stops. Determine the girl’s displacement from her initial point of departure.

18. Find a vector d⃗ $\overrightarrow{d}$ which is ⊥$\mathrm{\perp }$ to both a⃗ $\overrightarrow{a}$ and b⃗ $\overrightarrow{b}$ and c⃗ $\overrightarrow{c}$. d⃗ =15$\overrightarrow{d}=15$ Let a⃗ =i^+4j^+2k^,b⃗ =3i^−2j^+7k^$\overrightarrow{a}=\hat{i}+4\hat{j}+2\hat{k},\overrightarrow{b}=3\hat{i}-2\hat{j}+7\hat{k}$ and c⃗ =2i^−j^+4k^$\overrightarrow{c}=2\hat{i}-\hat{j}+4\hat{k}$.

CBSE Test Paper 01
Chapter 10 Vector Algebra

---

Solution

1. 4. π4$\frac{\pi }{4}$, Explanation: |a→|=3–√,|b→|=2,a→.b→=6–√$|\overrightarrow{a}|=\sqrt{3},|\overrightarrow{b}|=2,\overrightarrow{a}.\overrightarrow{b}=\sqrt{6}$
      ⇒a→.b→=|a→|.|b→|cosθ⇒6–√$\Rightarrow \overrightarrow{a}.\overrightarrow{b}=|\overrightarrow{a}|.|\overrightarrow{b}|\cos \theta \Rightarrow \sqrt{6}$
      =23–√cosθ$=2\sqrt{3}\cos \theta$
      ⇒cosθ=12√⇒θ=π4$\Rightarrow \cos \theta =\frac{1}{\sqrt{2}}\Rightarrow \theta =\frac{\pi }{4}$
2. 4. cos−1(57)${\cos }^{-1}\left(\frac{5}{7}\right)$, Explanation: a→=iˆ−2jˆ+3kˆ,b→=3iˆ−2jˆ+kˆ$\overrightarrow{a}=\hat{i}-2\hat{j}+3\hat{k},\overrightarrow{b}=3\hat{i}-2\hat{j}+\hat{k}$⇒|a→|=14−−√,|b→|=14−−√,a→.b→=10$\Rightarrow |\overrightarrow{a}|=\sqrt{14},|\overrightarrow{b}|=\sqrt{14},\overrightarrow{a}.\overrightarrow{b}=10$
      ⇒a→.b→|a→||b→|=cosθ⇒1014=cosθ$\Rightarrow \frac{\overrightarrow{a}.\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=\cos \theta \Rightarrow \frac{10}{14}=\cos \theta$
      ⇒cosθ=57⇒θ=cos−157$\Rightarrow \cos \theta =\frac{5}{7}\Rightarrow \theta ={\cos }^{-1}\frac{5}{7}$
3. 4. magnitude as well as direction, Explanation: A vector has both magnitude as well as direction.
4. 2. −4j^−k^$-4\hat{j}-\hat{k}$, Explanation: We have: vectors a⃗ =i^−2j^+k^,$\overrightarrow{a}=\hat{i}-2\hat{j}+\hat{k},$ b⃗ =−2i^+4j^+5k^$\overrightarrow{b}=-2\hat{i}+4\hat{j}+5\hat{k}$ and 
5. 1. 114√,214√,314√$\frac{1}{\sqrt{14}},\frac{2}{\sqrt{14}},\frac{3}{\sqrt{14}}$, Explanation: Let a→=i^+2j^+3k^$\overrightarrow{a}=\hat{i}+2\hat{j}+3\hat{k}$,

      Then, aˆ=a→∣∣a→∣∣=iˆ+2jˆ+3kˆ12+22+32√=iˆ+2jˆ+3kˆ14√$\hat{a}=\frac{\overrightarrow{a}}{\left|\overrightarrow{a}\right|}=\frac{\hat{i}+2\hat{j}+3\hat{k}}{\sqrt{1^2+2^2+3^2}}=\frac{\hat{i}+2\hat{j}+3\hat{k}}{\sqrt{14}}$
      Therefore , the D.C.’s of vector a are :
      114√,214√,314√.$\frac{1}{\sqrt{14}},\frac{2}{\sqrt{14}},\frac{3}{\sqrt{14}}.$

6. k ∈$\in$ ]-1, 1 [k ≠$\ne$ −12$-\frac{1}{2}$

7. 0

8. π3$\frac{\pi }{3}$

9. a⃗ ×b⃗ =∣∣∣∣∣i^23j^15k^3−2∣∣∣∣∣$\overrightarrow{a}\times \overrightarrow{b}=\left|\begin{array}{ccc}\hat{i}& \hat{j}& \hat{k}\\ 2& 1& 3\\ 3& 5& -2\end{array}\right|$
   =i^(−2−15)−j^(−4−9)+k^(10−3)$=\hat{i}\left(-2-15\right)-\hat{j}\left(-4-9\right)+\hat{k}\left(10-3\right)$
   =−17i^+13j^+7k^$=-17\hat{i}+13\hat{j}+7\hat{k}$
10. We are given that, a⃗ ⋅b⃗ =8$\overrightarrow{a}\cdot \overrightarrow{b}=8$ and b⃗ =2i^+6j^+3k^$\overrightarrow{b}=2\hat{i}+6\hat{j}+3\hat{k}$
    ∴$\therefore$ The projection of a⃗ $\overrightarrow{a}$ on b⃗ $\overrightarrow{b}$ is given as = a⃗ ⋅b⃗ |b⃗ |$\frac{\overrightarrow{a}\cdot \overrightarrow{b}}{|\overrightarrow{b}|}$
    =822+62+32√$=\frac{8}{\sqrt{2^2+6^2+3^2}}$
    =84+36+9√$=\frac{8}{\sqrt{4+36+9}}$
    =849√=87$=\frac{8}{\sqrt{49}}=\frac{8}{7}$
11. |a⃗ |=1$\left|\overrightarrow{a}\right|=1$
    (x⃗ −a⃗ ).(x⃗ +a⃗ )=8$\left(\overrightarrow{x}-\overrightarrow{a}\right).\left(\overrightarrow{x}+\overrightarrow{a}\right)=8$
    |x⃗ |2−|a⃗ |2=8${\left|\overrightarrow{x}\right|}^2-|\overrightarrow{a}{|}^2=8$
    |x⃗ |2−1=8${\left|\overrightarrow{x}\right|}^2-1=8$
    |x⃗ |2=9${\left|\overrightarrow{x}\right|}^2=9$
    |x⃗ |=3$\left|\overrightarrow{x}\right|=3$
12. Given: Point P (2, 3, 4) and Q(4,1, - 2)
    ∴$\therefore$ Position vector of point P is a⃗ =2i^+3j^+4k^$\overrightarrow{a}=2\hat{i}+3\hat{j}+4\hat{k}$
    And Position vector of point Q is b⃗ =4i^+j^−2k^$\overrightarrow{b}=4\hat{i}+\hat{j}-2\hat{k}$
    And Position vector of mid-point R of PQ is a⃗ +b⃗ 2=2i^+3j^+4k^+4i^+j^−2k^2$\frac{\overrightarrow{a}+\overrightarrow{b}}{2}=\frac{2\hat{i}+3\hat{j}+4\hat{k}+4\hat{i}+\hat{j}-2\hat{k}}{2}$
    =6i^+4j^+2k^2=3i^+2j^+k^$=\frac{6\hat{i}+4\hat{j}+2\hat{k}}{2}=3\hat{i}+2\hat{j}+\hat{k}$
13. a⃗ ×b⃗ =∣∣∣∣∣i^21j^−13k^32∣∣∣∣∣$\overrightarrow{a}\times \overrightarrow{b}=\left|\begin{array}{ccc}\hat{i}& \hat{j}& \hat{k}\\ 2& -1& 3\\ 1& 3& 2\end{array}\right|$
    =−11i^−j^+7k^$=-11\hat{i}-\hat{j}+7\hat{k}$
    ∣∣a⃗ ×b⃗ ∣∣=(−11)2+(−1)2+(7)2−−−−−−−−−−−−−−−−−−√$\left|\overrightarrow{a}\times \overrightarrow{b}\right|=\sqrt{{\left(-11\right)}^2+{\left(-1\right)}^2+{\left(7\right)}^2}$
    =171−−−√=319−−√$=\sqrt{171}=3\sqrt{19}$
    sinθ=∣∣a⃗ ×b⃗ ∣∣∣∣a⃗ ∣∣∣∣b⃗ ∣∣=319√14√.14√=31419−−√$\sin \theta =\frac{\left|\overrightarrow{a}\times \overrightarrow{b}\right|}{\left|\overrightarrow{a}\right|\left|\overrightarrow{b}\right|}=\frac{3\sqrt{19}}{\sqrt{14}.\sqrt{14}}=\frac{3}{14}\sqrt{19}$
14. Let a⃗ =i^+3j^+7k^$\overrightarrow{a}=\hat{i}+3\hat{j}+7\hat{k}$ and b⃗ =7i^−j^+8k^$\overrightarrow{b}=7\hat{i}-\hat{j}+8\hat{k}$
    Projection of vector a⃗ $\overrightarrow{a}$ on b⃗ =a⃗ .b⃗ ∣∣b⃗ ∣∣$\overrightarrow{b}=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{b}\right|}$
    =(1)(7)+(3)(−1)+7(8)(7)2+(−1)2+(8)2√$=\frac{\left(1\right)\left(7\right)+\left(3\right)\left(-1\right)+7\left(8\right)}{\sqrt{{\left(7\right)}^2+{\left(-1\right)}^2+{\left(8\right)}^2}}$
    =7−3+5649+61+64√=60114√$=\frac{7-3+56}{\sqrt{49+61+64}}=\frac{60}{\sqrt{114}}$
15. According to the question ,
    a⃗ =i^+j^+k^,$\overrightarrow{a}=\hat{i}+\hat{j}+\hat{k},$
    b⃗ =4i^−2j^+3k^$\overrightarrow{b}=4\hat{i}-2\hat{j}+3\hat{k}$ and
    c⃗ =i^−2j^+k^$\overrightarrow{c}=\hat{i}-2\hat{j}+\hat{k}$
    Now ,2a⃗ −b⃗ +3⃗ c⃗ $,2\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{3}\overrightarrow{c}$
    =2(i^+j^+k^)−(4i^−2j^+3k^)+3(i^−2j^+k^)$=2(\hat{i}+\hat{j}+\hat{k})-(4\hat{i}-2\hat{j}+3\hat{k})+3(\hat{i}-2\hat{j}+\hat{k})$
    =2i^+2j^+2k^−4i^+2j^−3k^+3i^−6j^+3k^$=2\hat{i}+2\hat{j}+2\hat{k}-4\hat{i}+2\hat{j}-3\hat{k}+3\hat{i}-6\hat{j}+3\hat{k}$
    =i^−2j^+2k^$=\hat{i}-2\hat{j}+2\hat{k}$
    ⇒2a⃗ −b⃗ +3c⃗ =i^−2j^+2k^$\Rightarrow 2\overrightarrow{a}-\overrightarrow{b}+3\overrightarrow{c}=\hat{i}-2\hat{j}+2\hat{k}$
    Now, a unit vector in the direction of vector is 2a⃗ −b⃗ +3c⃗ =2a⃗ −b⃗ +3c⃗ |2a⃗ −b⃗ +3c⃗ |$2\overrightarrow{a}-\overrightarrow{b}+3\overrightarrow{c}=\frac{2\overrightarrow{a}-\overrightarrow{b}+3\overrightarrow{c}}{|2\overrightarrow{a}-\overrightarrow{b}+3\overrightarrow{c}|}$
    =i^−2j^+2k^(1)2+(−2)2+(2)2√$=\frac{\hat{i}-2\hat{j}+2\hat{k}}{\sqrt{(1{)}^2+(-2{)}^2+(2{)}^2}}$
    =i^−2j^+2k^9√$=\frac{\hat{i}-2\hat{j}+2\hat{k}}{\sqrt{9}}$
    =i^−2j^+2k^3$=\frac{\hat{i}-2\hat{j}+2\hat{k}}{3}$
    =13i^−23j^+23k^$=\frac{1}{3}\hat{i}-\frac{2}{3}\hat{j}+\frac{2}{3}\hat{k}$
    Vector of magnitude 6 units parallel to the vector is ,
    =6(13i^−23j^+23k^)$=6\left(\frac{1}{3}\hat{i}-\frac{2}{3}\hat{j}+\frac{2}{3}\hat{k}\right)$
    =2i^−4j^+4k^$=2\hat{i}-4\hat{j}+4\hat{k}$
16. Given: Vectors a⃗ =i^+4j^+2k^$\overrightarrow{a}=\hat{i}+4\hat{j}+2\hat{k}$ and b⃗ =3i^−2j^+7k^$\overrightarrow{b}=3\hat{i}-2\hat{j}+7\hat{k}$
    We know that the cross-product of two vectors, a⃗ ×b⃗ $\overrightarrow{a}\times \overrightarrow{b}$ is a vector perpendicular to both a⃗ $\overrightarrow{a}$ and b⃗ $\overrightarrow{b}$
    Hence, vector d⃗ $\overrightarrow{d}$ which is also perpendicular to both a⃗ $\overrightarrow{a}$ and b⃗ $\overrightarrow{b}$ is d⃗ =λ(a⃗ ×b⃗ )$\overrightarrow{d}=\lambda \left(\overrightarrow{a}\times \overrightarrow{b}\right)$ where λ=1$\lambda =1$ or some other scalar.
    Therefore, d⃗ =λ∣∣∣∣∣i⃗ 13j⃗ 4−2k⃗ 27∣∣∣∣∣$\overrightarrow{d}=\lambda \left|\begin{array}{ccc}\overrightarrow{i}& \overrightarrow{j}& \overrightarrow{k}\\ 1& 4& 2\\ 3& -2& 7\end{array}\right|$
    =λ[i^(28+4)−j^(7−6)+k^(−2−12)]$=\lambda \left[\hat{i}\left(28+4\right)-\hat{j}\left(7-6\right)+\hat{k}\left(-2-12\right)\right]$
    ⇒d⃗ =32λi^−λj^−14λk^$\Rightarrow \overrightarrow{d}=32\lambda \hat{i}-\lambda \hat{j}-14\lambda \hat{k}$...(i)
    Now given c⃗ =2i^−j^+4k^$\overrightarrow{c}=2\hat{i}-\hat{j}+4\hat{k}$ and c⃗ .d⃗ =15$\overrightarrow{c}.\overrightarrow{d}=15$
    c⃗ .d⃗ =15$\overrightarrow{c}.\overrightarrow{d}=15$
    =2(32λ)+(−1)(−λ)+4(−14λ)=15$=2\left(32\lambda \right)+\left(-1\right)\left(-\lambda \right)+4\left(-14\lambda \right)=15$
    ⇒64λ+λ−56λ=15$\Rightarrow 64\lambda +\lambda -56\lambda =15$
    ⇒9λ=15$\Rightarrow 9\lambda =15$
    ⇒λ=159$\Rightarrow \lambda =\frac{15}{9}$
    ⇒λ=53$\Rightarrow \lambda =\frac{5}{3}$
    Putting λ=53$\lambda =\frac{5}{3}$ in eq. (i), we get
    d⃗ =53[32i^−j^−14k^]$\overrightarrow{d}=\frac{5}{3}\left[32\hat{i}-\hat{j}-14\hat{k}\right]$
    ⇒d⃗ =13[160i^−5j^−70k^]$\Rightarrow \overrightarrow{d}=\frac{1}{3}\left[160\hat{i}-5\hat{j}-70\hat{k}\right]$
17. Let the initial point of departure is origin (0, 0) and the girl walks a distance OA = 4 km towards west.
    Through the point A, draw a line AQ parallel to a line OP, which is 300${30}^0$ East of North, i.e., in East-North quadrant making an angle of 300${30}^0$ with North.
    Again, let the girl walks a distance AB = 3 km along this direction OQ−→−$\overrightarrow{OQ}$
    ∴OA−→−=4(−i⃗ )=−4i^$\therefore \overrightarrow{OA}=4\left(-\overrightarrow{i}\right)=-4\hat{i}$ …(i) [∵$\because$ Vector OA−→−$\overrightarrow{OA}$ is along OX’]
    
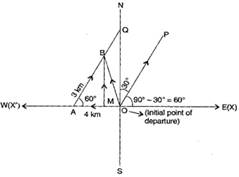
    Now, draw BM perpendicular to x - axis.
    In ΔAMB$\mathrm{\Delta }AMB$ by Triangle Law of Addition of vectors,
    AB−→−=AM−→−+MB−→−=(AM)i^+(MB)i^$\overrightarrow{AB}=\overrightarrow{AM}+\overrightarrow{MB}=\left(AM\right)\hat{i}+\left(MB\right)\hat{i}$
    Dividing and multiplying by AB in R.H.S.,
    AB−→−=ABAMABi^+ABMBABj^$\overrightarrow{AB}=AB\frac{AM}{AB}\hat{i}+AB\frac{MB}{AB}\hat{j}$ =3cos60oi^+3sin60oj^$=3\cos {60}^o\hat{i}+3\sin {60}^o\hat{j}$
    ⇒AB=312i^+33√2i^=32i^+33√2j$\Rightarrow AB=3\frac{1}{2}\hat{i}+3\frac{\sqrt{3}}{2}\hat{i}=\frac{3}{2}\hat{i}+\frac{3\sqrt{3}}{2}j$ …(ii)
    ∴$\therefore$ Girl’s displacement from her initial point O of departure to final point B,
    OB−→−=OA−→−+AB−→−$\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}$ =−4i^+(32i^+32√2j^)$=-4\hat{i}+\left(\frac{3}{2}\hat{i}+\frac{3\sqrt{2}}{2}\hat{j}\right)$ =(−4+32)i^+33√2j^$=\left(-4+\frac{3}{2}\right)\hat{i}+\frac{3\sqrt{3}}{2}\hat{j}$
    ⇒OB−→−=−52i^+33√2j^$\Rightarrow \overrightarrow{OB}=\frac{-5}{2}\hat{i}+\frac{3\sqrt{3}}{2}\hat{j}$
18. a⃗ =i^+4j^+2k^,b⃗ =3i^−2j^+7k^$\overrightarrow{a}=\hat{i}+4\hat{j}+2\hat{k},\overrightarrow{b}=3\hat{i}-2\hat{j}+7\hat{k}$ and c⃗ =2i^−j^+4k^$\overrightarrow{c}=2\hat{i}-\hat{j}+4\hat{k}$
    Let d⃗ =xi^+yj^+zk^$\overrightarrow{d}=x\hat{i}+y\hat{j}+z\hat{k}$
    ATQ, d⃗ .a⃗ =0,d⃗ .b⃗ =0$\overrightarrow{d}.\overrightarrow{a}=0,\overrightarrow{d}.\overrightarrow{b}=0$ and c⃗ .d⃗ =15$\overrightarrow{c}.\overrightarrow{d}=15$, then,
    x + 4y + 2z = 0 ...(1)
    3x - 2y + 7z = 0 ...(2)
    2x - y + 4z = 15 ...(3)
    On solving equation (1) and (2)
    
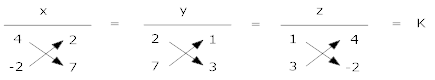
    x28+4=y6−7=z−2−12=k$\frac{x}{28+4}=\frac{y}{6-7}=\frac{z}{-2-12}=k$
    x = 32k, y = -k, z = -14k
    Put x, y, z in equation (3)
    2(32k) - (-k) + 4(-14k) = 15
    64k + k - 56k = 15
    9k = 15
    k=159$k=\frac{15}{9}$
    k=53$k=\frac{5}{3}$
    x=32×53=1603$x=32\times \frac{5}{3}=\frac{160}{3}$
    y=−53$y=-\frac{5}{3}$
    z=−14×53=−703$z=-14\times \frac{5}{3}=-\frac{70}{3}$
    d⃗ =1603i^−53j^−703k^