Vector Algebra - Revision Notes

CBSE Class 12 Mathematics
Chapter-10
Vector Algebra

---

• Vector: A quantity that has magnitude as well as direction is called vector.
• Zero Vector: A vector whose intial and terminal point coincide is called a zero vector or a null vector. It is denoted as O→$\overrightarrow{\mathrm{O}}$.
• Co-initial vectors: Two or more vectors having the same initial points are called co-initial vectors.
• Collinear vectors: Two or more vectors are said to be collinear if they are parallel to the same line, irrespective of their magnitudes and directions.
• Equal vectors: Two vectors are said to be equal, if they have the same magnitude and direction regardless of the position of their initial points.
• Negative of a vector: A vector whose magnitude is the same as that of a given vector, but direction is opposite to that of it, is called negative of the given vector.
• Position vector of a point P (x, y) is given as OP−→−(=r→)=xiˆ+yjˆ+zkˆ$\overrightarrow{\mathrm{O}\mathrm{P}}\left(=\overrightarrow{r}\right)=x\hat{i}+y\hat{j}+z\hat{k}$  and its magnitude by 
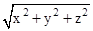
• The scalar components of a vector are its direction ratios, and represent its projections along the respective axes.
• The magnitude (r), direction ratios (a, b, c) and direction cosines (l, m, n) of any vector are related as: 
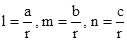
• The vector sum of the three sides of a triangle taken in order is  O→$\overrightarrow{\mathrm{O}}$  
• The vector sum of two conidial vectors is given by the diagonal of the parallelogram whose adjacent sides are the given vectors.
• The multiplication of a given vector by a scalar λ, changes the magnitude of the vector by the multiple |λ|, and keeps the direction same (or makes it opposite) according as the value of λ is positive (or negative).
• For a given vector a→$\overrightarrow{a}$, the vector aˆ=a→∣∣a→∣∣$\hat{a}=\frac{\overrightarrow{a}}{\left|\overrightarrow{a}\right|}$gives the unit vector in the direction of a→$\overrightarrow{a}$ 
• The position vector of a point R dividing a line segment joining the points P and Q whose position vectors are  a→$\overrightarrow{a}$ and b→$\overrightarrow{b}$respectively, in the ratio 
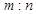
  (i)  internally, is given by na→+mb→m+n$\frac{n\overrightarrow{a}+m\overrightarrow{b}}{m+n}$ 
  (ii)  externally, is given by mb→−na→m−n$\frac{m\overrightarrow{b}-n\overrightarrow{a}}{m-n}$ 
• The scalar product of two given vectors a→$\overrightarrow{a}$ and b→$\overrightarrow{b}$ having angle θ between them is defined as a→.b→=∣∣a→∣∣∣∣∣b→∣∣∣cosθ$\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\right|\left|\overrightarrow{b}\right|\cos \theta$ 
  Also, when a→.b→$\overrightarrow{a}.\overrightarrow{b}$is given, the angle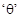 between the vectors a→$\overrightarrow{a}$ and b→$\overrightarrow{b}$ may be determined by cosθ=a→.b→∣∣a→∣∣∣∣∣b→∣∣∣$\cos \theta =\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|\left|\overrightarrow{b}\right|}$ 
• If 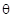 is the angle between two vector  a→$\overrightarrow{a}$ and b→$\overrightarrow{b}$,  then their cross product is given as
  a→×b→=∣∣a→∣∣∣∣∣b→∣∣∣sinθ.nˆ$\overrightarrow{a}\times \overrightarrow{b}=\left|\overrightarrow{a}\right|\left|\overrightarrow{b}\right|\sin \theta .\hat{n}$where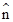is a unit vector perpendicular to the plane containing a→$\overrightarrow{a}$ and b→$\overrightarrow{b}$. Such that a→,b→,nˆ$\overrightarrow{a},\overrightarrow{b},\hat{n}$ form right handed system of coordinate axes.
• If we have two vectors  a→$\overrightarrow{a}$ and b→$\overrightarrow{b}$ given in component form as a→=a1iˆ+a2jˆ+a3kˆ$\overrightarrow{a}=a_1\hat{i}+a_2\hat{j}+a_3\hat{k}$  and  b→=b1iˆ+b2jˆ+b3kˆ$\overrightarrow{b}=b_1\hat{i}+b_2\hat{j}+b_3\hat{k}$  and λ$\lambda$ be  any scalar, then,
  a→+b→=(a1+b1)iˆ+(a2+b2)jˆ+(a3+b3)kˆ$\overrightarrow{a}+\overrightarrow{b}=\left(a_1+b_1\right)\hat{i}+\left(a_2+b_2\right)\hat{j}+\left(a_3+b_3\right)\hat{k}$
  λa→=(λa1)iˆ+(λa2)jˆ+(λa3)kˆ$\lambda \overrightarrow{a}=\left(\lambda a_1\right)\hat{i}+\left(\lambda a_2\right)\hat{j}+\left(\lambda a_3\right)\hat{k}$
  a→.b→=a1b1+a2b2+a3b3$\overrightarrow{a}.\overrightarrow{b}=a_1{b}_1+a_2{b}_2+a_3{b}_3$
  
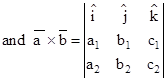
  Parallelogram Law of vector addition: If two vectors a→$\overrightarrow{a}$ and b→$\overrightarrow{b}$ are represented by adjacent sides of a parallelogram in magnitude and direction, then their sum a→+b→$\overrightarrow{a}+\overrightarrow{b}$ is represented in magnitude and direction by the diagonal of the parallelogram through their common initial point. This is known as Parallelogram Law of vector addition.